对于如TLS流量、医疗数据库、区块链等等许多需要高度保障安全的应用方向,前向保密绝对必不可少,但仅仅防止黑客快速解密敏感信息是远远不够的,威胁模型还应该考虑攻击者在收集密文多年之后解开密文的情况。
可能打破的前方保密的潜在方式是:增加的计算能力和数量基础理论的突破,这会使攻击密码变的很简单。
但是,除非有人找到了用于分解大整数的多项式时间算法,否则这种风险对于当前的密码算法来说可能性很小,我们应该更关注量子计算机的成功开发。
量子计算入门
量子计算机不仅仅是大规模并行的经典计算机。人们常常认为,由于量子比特可以同时占据0和1,因此n比特量子计算机可以同时处于2 n个状态,因此可以非常快速地计算NP。
其实情况并非如此,因为测量量子态会破坏大部分原始信息。例如,量子系统完全了解物体的动量和位置,但任何动量测量都会破坏有关位置的信息,反之亦然。这被称为海森堡不确定性原理。
因此,成功的量子算法由量子比特的一系列变换组成,使得在计算结束时,测量系统的状态不会破坏所需的信息。事实上,已经证明,不存在量子算法同时尝试解决某些NP完全问题并输出正确的量子算法。换句话说,任何用于解决硬经典问题的量子算法都必须利用具体结构。
今天,有两种这样的算法可用于密码分析。
快速计算大数的能力将破坏RSA和离散的基于日志的加密。整数分解的最快算法是一般数字域筛,它在亚指数时间内运行。
在1994年,Peter Shor开发了一种用于整数分解的量子算法(Shor算法),该算法在多项式时间内运行,因此能够破坏任何RSA或离散的基于对象的密码系统(包括那些使用椭圆曲线的密码系统)。这意味着如果有人要构建量子计算机,那么所有广泛使用的公钥密码都是不安全的。
第二个是Grover的算法,它能够在O(√n)时间内反转函数。该算法会通过根因子降低对称密钥加密的安全性,因此AES-256只能提供128位的安全性。类似地,找到256位散列函数的前映像只需要2 128次。由于将哈希函数或AES的安全性提高两倍并不是非常繁琐,因此Grover的算法不会对对称加密造成严重威胁。此外,建议用于加密使用的伪随机数发生器都不会受到量子计算机发明的影响,除非Grover算法引起的O(√n)因子。
后量子算法的类型
后量子密码学是对密码系统的研究,它可以在经典计算机上运行,即使对手拥有量子计算机也是绝对安全的。
最近,NIST启动了标准化后量子加密的过程,目前正在审查第一轮提交。这些提交中最有希望的包括基于格,同源,Hash函数和编码的密码系统。
在深入研究每类提交之前,我们简要总结一下每种类型的密码系统固有的权衡,并与当前(非后量子)椭圆曲线密码学进行比较。请注意,代码和同基因能够生成数字签名,但没有向NIST提交此类方案。
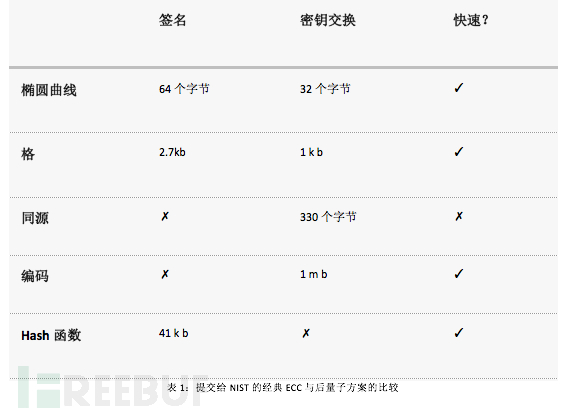
在安全性证明方面,上述密码系统都没有减少到NP-Hard(或NP完全)问题。在格和编码的情况下,这些密码系统基于NP难问题的轻微修改。基于散列的构造依赖于良好散列函数的存在,并且不进行其他加密假设。
最后,基于同基因的密码学基于一个被推测为难的问题,但与NP-Hard问题或先前的加密假设不相似。然而,值得一提的是,正如我们无法证明任何经典算法在多项式时间内都不易破碎(因为P可能等于NP),可能是量子计算机认为难以解决的问题。此外,一个不会减少到一些NP难或完整问题的密码系统本身不应该是一个标记。
格
在后量子加密的所有方法中,对格子的研究是最活跃和最灵活的。它们具有很强的安全性,可以进行密钥交换,数字签名以及完全同态加密等更复杂的构造。尽管格子密码系统的优化和安全性证明都需要极其复杂的数学,但基本思想只需要基本的线性代数。假设您有一个形式的线性方程组,比如说:
求解x是一个经典的线性代数问题,可以使用高斯消元法快速求解。
另一种思考方式是我们有一个神秘的功能:
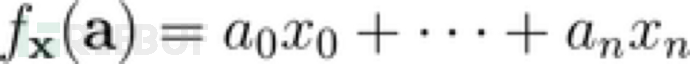
给定一个向量的地方a,我们看到了结果ax,而不知道x。在查询此函数足够多次后,我们可以在很短的时间内得到f(通过求解上面的方程组)。这样我们就可以将线性代数问题重新定义为机器学习问题。
现在,假设我们引入少量噪声到我们的功能,使相乘后x和a,我们增加一个误差项e,降低了整个事情的一个模(中型)q
![]()
学习这种带噪的神秘函数已经在数学上被证明是非常困难的。直觉是在我们在非噪声情况下使用的高斯消除过程的每一步中,误差项变得越来越大,直到它超越了关于函数的所有有用信息。在密码学文献中,这被称为带有错误学习问题(LWE)。
基于LWE的密码学被称为基于格的密码学的原因,已知NP-Hard,LWE难以证明依赖于在称为格子的东西中找到最短向量。我们不会在这里深入研究格子的数学,但可以认为格子是n维空间的平铺:
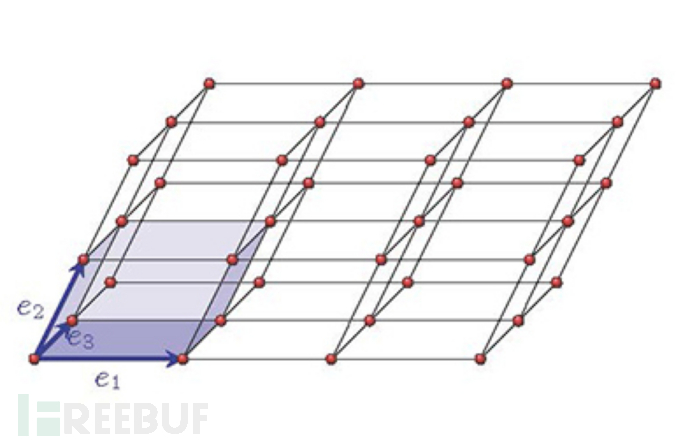
格子由坐标向量表示。在上面的例子中,晶格的任何点可通过将达到(经由正常矢量相加)。最短向量问题(SVP)说:给定一个点阵,找到长度为向量的元素最短。很难的直观原因是并非所有给定晶格的坐标系都同样易于使用。在上面的例子中,我们可以用三个非常长且靠近的坐标向量来表示晶格,这使得寻找靠近原点的向量更加困难。事实上,有一种规范的方法可以找到格子的“最坏可能”表示。当使用这样的表示时,已知最短向量问题是NP-hard。
在研究如何使用LWE进行抗量子密码学之前,我们应该指出LWE本身不是NP-Hard。它不是直接降低到SVP,而是降到SVP的近似值,推测它是不是NP-Hard。尽管如此,目前还没有用于求解LWE的多项式(或次指数)算法。
现在让我们使用LWE问题来创建一个实际的密码系统。最简单的方案是由Oded Regev在他的原始论文中创建的,证明了LWE问题的硬度。这里,秘密密钥是具有整数条目mod的n维向量q,即上面提到的LWE秘密。公钥是A前面讨论的矩阵,以及LWE函数的输出向量:
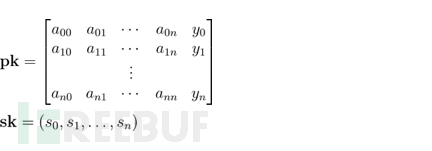
这个公钥的一个重要特性是,当它乘以向量时,我们得到了大致的误差项:(-sk,1)0。
为了加密一些信息m,我们取结果的最后一个坐标中的随机列A和编码的总和,m加上0,如果m是0,q/2如果m是1。换句话说,我们选择x0或1 的随机向量,并进行计算:
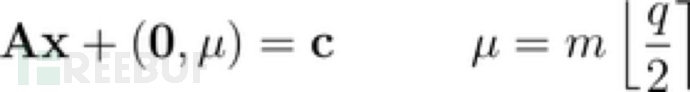
直觉上,我们刚刚评估了LWE函数(我们知道它很难破解)并在此函数的输出中编码了我们的位。
解密是有效的,因为知道LWE秘密将允许收件人收回消息,加上一个小错误术语:
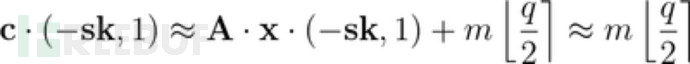
正确选择错误分布后,它永远不会使消息失真超过q/4。接收方可以测试输出是否更接近0或相应地q/2 mod q解码该位。
该系统的一个主要问题是它具有非常大的密钥。要加密一位信息,需要安全参数中大小为n 2的公钥。然而,格子密码系统的一个吸引人的方面是它们非常快。
自Regev的原始论文以来,围绕基于格的密码系统进行了大量工作。改进其实用性的关键突破是Ring-LWE的开发,这是LWE问题的变体,其中键由某些多项式表示。这导致密钥大小的二次减少,加速加密和解密,仅使用n*log(n)操作(使用快速傅立叶技术)。
在考虑用于NIST PQC标准的许多基于晶格的密码系统中,特别值得一提的两个是晶体结构,Kyber和Dilithium。
Kyber是一种密钥封装机制(KEM),它遵循与上述系统类似的结构,但使用一些花哨的代数数论来获得比Ring-LWE更好的性能。对于合理的安全参数,密钥大小约为1kb(仍然很大!)但加密和解密时间大约为0.075毫秒。考虑到这种速度是通过软件实现的,Kyber KEM似乎很有希望进行后量子密钥交换。
Dilithium是一种基于类似Kyber技术的数字签名方案。它的详细信息超出了本博文的范围,但值得一提的是它也实现了相当不错的性能。公钥大小约为1kb,签名为2kb。它也非常高效。在Skylake处理器上,计算签名所需的平均周期数约为200万。验证平均需要390,000个周期。
编码
纠错码的研究在计算机科学文献中有着悠久的历史,可以追溯到Richard Hamming和Claude Shannon的突破性工作。我们无法在一篇简短的博文中开始研究这个深层领域的表面,但我们会给出一个快速概述。
在传递二进制消息时,错误可能以位翻转的形式发生。纠错码提供了以消息紧凑性为代价承受一定数量的位翻转的能力。例如,我们可以通过将0编码为000而将1编码为111来防止单比特翻转。这样,接收器可以通过对三个比特进行多数表决来确定101实际上是111,或者001是0。但是,这个编码无法纠正两个位被翻转的错误,因为转换为001的111将被解码为0。
最突出的纠错码类型称为线性码,可以用k x n矩阵表示,其中k是原始消息n的长度,是编码消息的长度。通常,在不知道底层线性编码的情况下解码消息在计算上是困难的。这种硬度巩固了McEliece公钥密码系统的安全性。
在高级别,McEliece系统中的秘密密钥是G来自称为Goppa码的一类代码的随机码(表示为矩阵)。公钥是矩阵SGP,其中S是具有二进制条目的可逆矩阵并且P是置换。为了加密消息m,发送方计算c = m(SGP) + e,其中e是随机错误向量,其中包含编码能够纠正的错误数量。为了解密,我们进行计算,这样就可以纠正添加的错误术语。通过计算可以轻松恢复该消息:cP-1 = mSG + eP-1mSGemSS-1。
与格子一样,基于代码的密码术也存在密钥是大矩阵的事实。使用推荐的安全参数,McEliece公钥大约为1 MB,私钥为11 kb。目前正在尝试使用称为准循环中等密度奇偶校验码的特殊类代码,这些代码可以比Goppa代码更简洁地表示,但是这些便阿门的安全性比Goppa码的研究更少。
同源
椭圆曲线密码学领域因使用相当多的奥术数学而臭名昭着。同基因将这一点提升到一个全新的水平。在椭圆曲线加密中,我们使用Diffie-Hellman类型协议来获取共享秘密,但是我们不是将组元素提升到某个幂,而是遍历椭圆曲线上的点。在基于同源的密码学中,我们再次使用Diffie-Hellman类型协议,但我们不是通过椭圆曲线上的点遍历,而是通过一系列椭圆曲线本身。
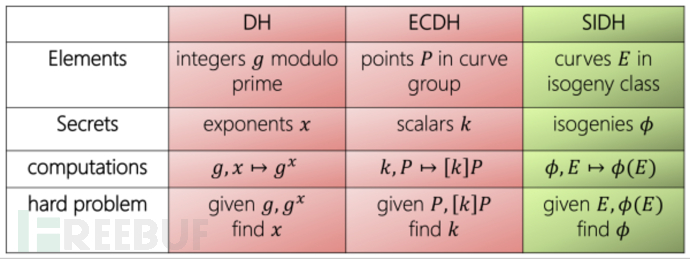
同种映射变换,使得上述第一曲线的组结构被反映在第二椭圆曲线到另一个的功能。对于那些熟悉群论的人来说,它是一个群同态,有一些附加的结构来处理每条曲线的几何。当我们将注意力限制在超奇异椭圆曲线(我们在此不会定义)时,每条曲线都保证从其到其他超奇异曲线具有固定数量的同胚。
现在,考虑通过从我们的起始曲线检查该形式的所有同基因,然后从这些曲线中检查所有同基因来创建的图,依此类推。这个图表在高度结构化的意义上说,如果我们从第一条曲线开始随机游走,击中特定其他曲线的概率可以忽略不计(除非我们采取指数级的步骤)。在数学术语中,我们说通过检查所有这些同源生成的图是一个扩展图(以及Ramanujan)。这种扩展特性正是使基于同源的密码学安全的原因。
对于超奇异同源 Diffie-Hellman(SIDH)方案,密钥是同源链,公钥是曲线。当Alice和Bob组合这些信息时,他们会获得不同的曲线,但具有相同的不变量。对于加密的目的而言,j-invariant不是那么重要,而是它是Alice和Bob完成密钥交换后可以很容易地计算的数字。
与其他后量子方案相比,基于同源的密码学具有极小的密钥大小,仅使用330个字节用于公钥。不幸的是,在这篇文章中讨论的所有技术中,它们是最慢的,对于密钥生成和共享秘密计算都需要11-13毫秒。然而,他们确实支持完美的前向保密,这不是其他后量子密码系统所拥有的。
基于Hash的签名
已经有许多基于哈希的签名的友好介绍,所以我们对它们的讨论相当高级。简而言之,哈希签名使用哈希函数的输入作为密钥并输出作为公钥。这些密钥仅适用于一个签名,因为签名本身会显示密钥的一部分。基于散列的签名的极端低效导致区块链使用Merkle树来减少空间消耗(是的,比特币中使用的相同Merkle树)。
不幸的是,用哈希构造KEM或公钥加密方案是不可能的。因此,基于散列的签名不是完整的后量子密码学的解决方案。而且,它们不是空间有效的; 一种更有前途的签名方案SPHINCS产生41kb的签名和1kb的公钥/私钥。另一方面,基于散列的方案非常快,因为它们只需要计算散列函数。它们还具有极强的安全性证据,完全基于存在具有抗冲突和抗图像抗性的散列函数的假设。由于没有任何迹象表明当前广泛使用的哈希函数(如SHA3或BLAKE2)容易受到这些攻击,因此基于哈希的签名是安全的。
小贴士
后量子密码学是一个令人难以置信又令人兴奋的研究领域,在过去十年中已经取得了巨大的增长。虽然这篇文章中描述的四种类型的密码系统已经得到了很多学术上的关注,但是没有一种被NIST批准,因此不推荐用于一般用途。许多方案的原始形式不具备性能,并且受到各种优化的影响,这些优化可能会或可能不会影响安全性。实际上,已经证明多次尝试为McEliece系统使用更节省空间的代码是不安全的。就目前而言,从后量子密码系统中获得最佳安全性需要牺牲一些空间或时间。基于环形点阵的密码学是灵活性方面最有前途的工作途径(签名和KEM,也是完全同态加密),但它所基于的假设仅在几年内得到了强烈的研究。现在,最安全的赌注是使用McEliece和Goppa代码,因为它已经经受了数十年的密码分析。
*本文来源:Trailofbits blog,编译:猎豹区块链安全实验室,转载请注明来自FreeBuf.COM





