前言

最近打了几个内部比赛题目，发现android类题目中，des算法加密的比重迅速上升。遂吸引到我们来深入了解一下des算法。百度搜了一下目前关于des的优质ctf题目相对来说比较少那么从何开始呢？

众所周知 CTF圈内有一名很出名的厨子（23333）他擅长各种加解密，没错就是我们常用的cyberchef工具，于是我们突发奇想，cyberchef列举的des加密的形式够全面了吧？不如跟着他来学习一下des加密

DES算法原理

前置概念：Feistel网络

DES加密的结构，也称为Feistel网络。在Feistel网络中，加密的各个步骤称为轮，整个加密过程就是进行若干次轮的循环。加密的每一轮都需要使用一个不同的子密钥

轮函数的作用是根据右侧和子密钥生成对左侧进行加密的比特序列，它是密码系统的核心。

一轮的具体计算步骤简要如下：

将输入的数据等分为左右两部分
将输入的右侧直接发送到输出的右侧
将输入的右侧发送到轮函数
轮函数根据右侧数据和子密钥，计算出一串看上去是随机的比特序列
将上一步得到的比特序列与左侧数据进行xor运算，并将结果作为加密后的左侧

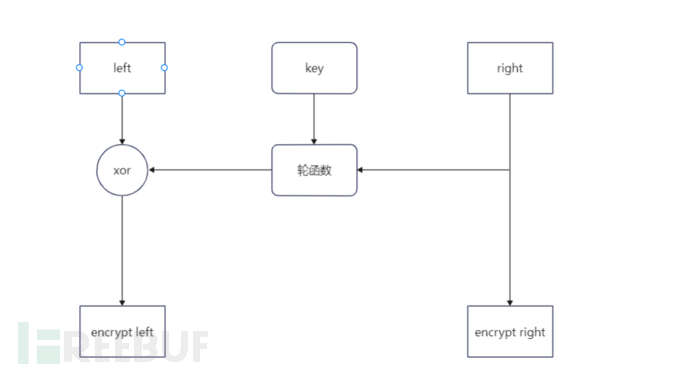
不难发现这种加密存在一定的问题：右侧的数据根本就没有加密。那么des算法是如何解决这个问题的呢？看完下文DES加密过程分析你就明白了

探秘DES!

DES 全称为 Data Encryption Standard，即数据加密标准，是一种使用密钥加密的块算法。

DES 算法就是一个把 8 字节 64 位的明文输入块变为 64 位密文输出块的算法，它所使用的密钥也是 64 位（其实只使用到了 56 位，其余 8 位为奇偶校验位）

算法特点：分组比较短、密钥太短、密码生命周期短、运算速度较慢。

DES 算法的控制参数有三个：Key、Data、Mode

Key（密钥）：为 7 个字节共 56 位，是 DES 算法的工作密钥（若说密钥为 64 位，其指的也是 56 位的秘钥加上 8 位奇偶校验位，奇偶校验位为第 8,16,24,32,40,48,56,64 位）

Data（数据）：为 8 个字节 64 位，是要被加密或被解密的数据

Mode（模式）： 为 DES 的工作方式，有两种：encrypt或decrypt。

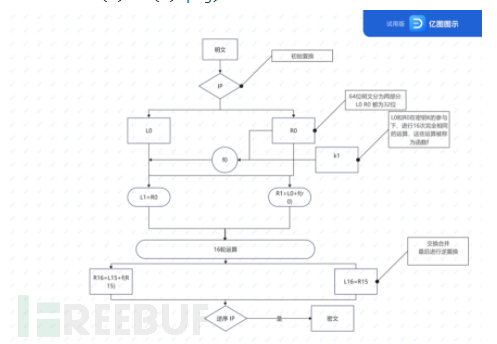
简单来说，可以将des加密总结为如下四个阶段

初始置换阶段：
输入密钥 64位
根据置换选择表得到密钥 28位*2
根据循环左移表，将密钥循环左移
将两个分开的密钥合并成56位，根据置换选择表2得到48位的子密钥
回到第三步根据轮数进行不同的左移，知道循环16轮，产生16个子密钥

初始明文处理阶段：
明文初始置换 64位
置换后的明文分为两组 32位*2

加密阶段：
对经过初始置换并分组的明文的一组进行E-盒拓展为48位
将拓展后的明文同对应的子密钥进行异或得到密文 48位
密文经过S-盒由48位变为32位
32位的密文经过P-盒乱序
交换左右两分组，进入下一轮加密阶段，整个加密阶段循环16轮

最后密文逆置换阶段：
将以上操作所得的密文进行逆置换得到最终的密文

接下来详细讲一讲初始置换阶段和加密阶段

初始置换阶段

例如置换顺序表如下：

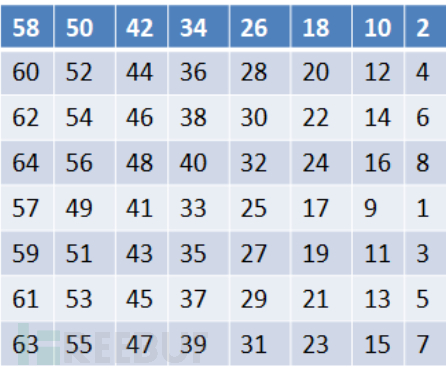
测试原文："abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789+="

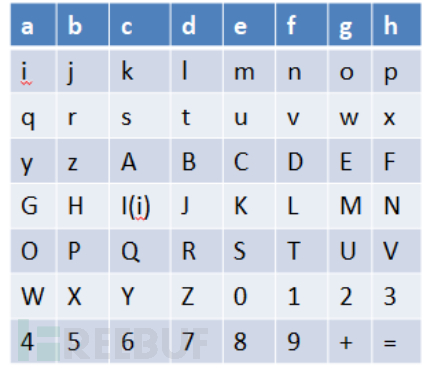
这样a就填到置换顺序表的“1”位置，b就填到“2”位置。以此类推，那么初始置换后就是这样的

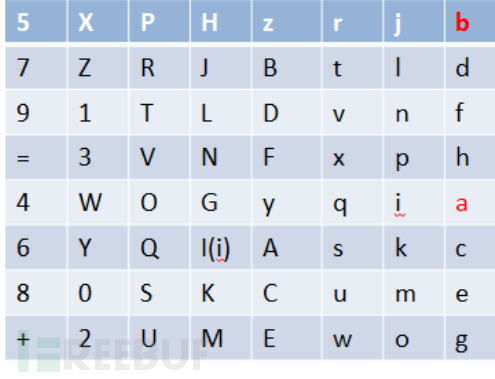
这样我们就能够得到处理过的明文：

“5XPHzrjb7ZRJBtld91TLDvnf=3VNFxph4WOGyqia6YQI(i)Askc80SKCume+2UMEwog”

然后我们就进入明文处理阶段。初始置换完成之后，需要将置换后的数据分为 L0、R0：

L0 = “5XPHzrjb7ZRJBtld91TLDvnf=3VNFxph”

R0 = “4WOGyqia6YQI(i)Askc80SKCume+2UMEwog”

加密阶段

加密阶段主要依赖函数f进行处理。函数f的加密流程参照我们之前了解过的Feistel网络的模型，现在我们解决上面遗留的问题，如何解决右侧数据没有加密的问题呢？

Feistel加密过程：

1. 先对其进行扩展置换，使其变为 48 位的数据，
2. 然后生成的数据再与子密钥进行异或运算，得到一组新的 48 位数据
3. 再以异或运算后的 48 位数据进行 S 盒代替，将 48 位的数据，转换为 32 位的数据，
4. 再进行 P 盒置换，生成 32 位的数据
5. 最后将 P 盒置换生成的数据与本轮运算时输入的 L 进行异或运算，生成新的 R。
6. 而新的 L 是直接由本轮的 R 进行替换

扩展置换 E：

扩展置换的作用对象是我们在初始置换后，将数据拆分为两部分（L,R）中的右半部分 R。

扩展置换表如下：

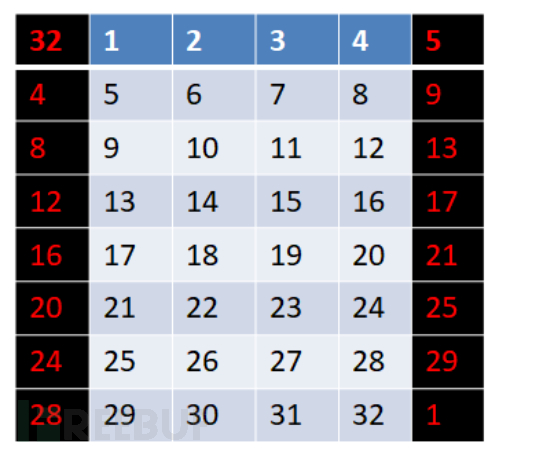将数据 R（32位），按照每 4 位一组，拆分成 8 个组，如图，左右两侧黑色的两列是扩展时添加的数据，中间的就是分组后的数据 R，表中的数字代表数据 R 中的位置。分成 8 组后，遵循这样的一个规则得到新的密文：

1.每一组的头部添加本组数据上一组的尾部，
2. 每一组的尾部添加本组数据下一组的头部。
即第一组数据，前面添加的是最后一组的最后一位数据，后面添加的是第二组的第一位数据

子密钥生成

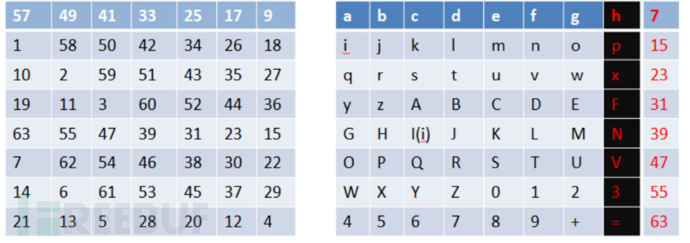
子秘钥 K 的生成靠的是两次压缩置换，下面讲一下压缩置换的原理

将64位数据每8位分成一组，每一组的最后一位数据作为奇偶校验位不参与加密运算，接着跟之前讲过的初始置换一样，将字母换到对应的位置上就可以了。

S 盒代替：

在RC4算法的学习当中，我们就接触过s盒这个概念了。

S 盒代替的作用，就是将我们上一步，R0 与 K1 异或后得到的 48 位数据压缩为 32 位数据。

下面语言描述一下s盒代替的过程

S 盒一共有 8 个，每一个都是一个 4 行 16 列的数组。将得到的 R0 平均分为 8 组，每组对应一个 S 盒。每一组的数据长度为 6 位
假设第一组的二进制数据为：“101011”
那么，我们取第一位与最后一位，组成十进制行数：“11”=3
然后取中间四位，组成十进制列数：“0101”=5
接着在对应的 S1 盒中，取 3 行 5 列的数据（第 4 行第 6 列）
再将取得的数字转换为 2 进制，将这个得到的4位二进制数据，代替原来第一组的 6 位数据，这样一来，等 8 个S盒全部代替完毕，我们就得到 32 位的数据

P 盒置换

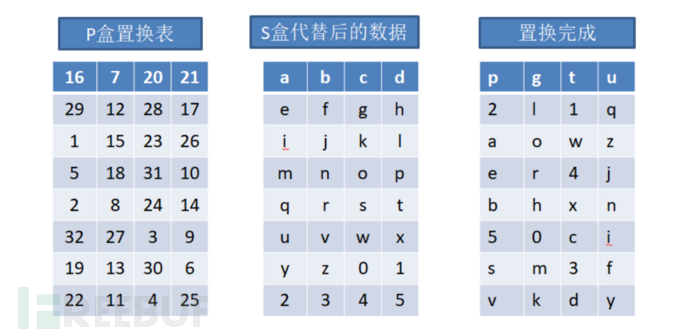
S 盒置换完成之后，要进行的就是 P 盒置换了，p盒置换不牵扯数据压缩的问题，输入 32 位的数据，得到 32 位的输出。下面我们放张图来解释这个简单替换过程

des加密模式辨析

ECB-电子密码本模式

最古老,最简单的模式，将加密的数据分成若干组，每组的大小跟加密密钥长度相同；

然后每组都用相同的密钥加密, 比如DES算法, 如果最后一个分组长度不够64位,要补齐64位；

定义:

​ Enc(X,Y)是加密函数

​ Dec(X,Y)是解密函数

​ Key是加密密钥；

​ Pi ( i = 0,1…n)是明文块，大小为64bit；

​ Ci ( i = 0,1…n)是密文块，大小为64bit;

ECB加密算法可表示为：

​ Ci = Enc(Key, Pi)

ECB解密算法可以表示为：

​ Pi = Dec(Key,Ci)

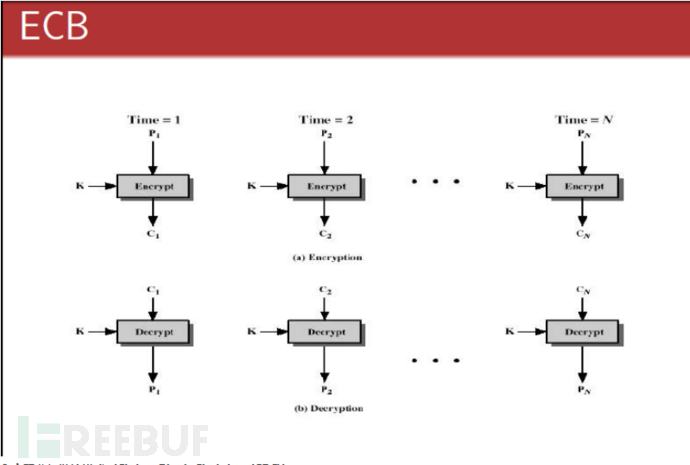
算法 特点:

• 每次Key、明文、密文的长度都必须是64位；

• 数据块重复排序不需要检测；

• 相同的明文块(使用相同的密钥)产生相同的密文块，容易遭受字典攻击；

• 一个错误仅仅会对一个密文块产生影响；

CBC-加密块链模式

与ECB模式最大的不同是加入了初始向量

定义：

​ Enc(X,Y)是加密函数

​ Dec(X,Y)是解密函数

​ Key是加密密钥；

​ Pi ( i = 0,1…n)是明文块，大小为64bit；

​ Ci ( i = 0,1…n)是密文块，大小为64bit;

​ XOR(X,Y)是异或运算；

​ IV是初始向量（一般为64位）；

ECB加密算法可表示为：

​ C0 = Enc(Key, XOR(IV, P0)

​ Ci = Enc(Key, XOR(Ci-1, Pi)

ECB解密算法可以表示为：

​ P0 = XOR(IV, Dec(Key, C0))

​ Pi = XOR(Ci-1, Dec(Key,Ci))

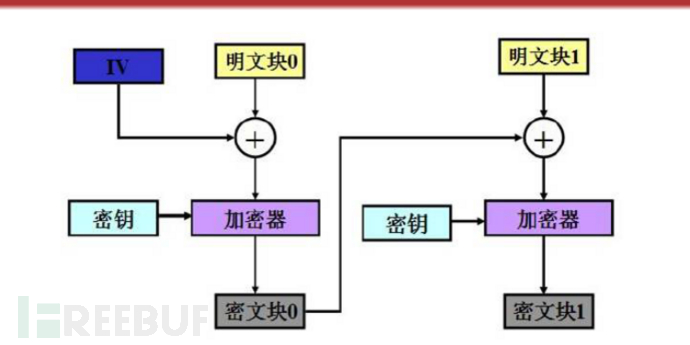
算法特点:

• 每次加密的密文长度为64位(8个字节);

• 当相同的明文使用相同的密钥和初始向量的时候CBC模式总是产生相同的密文;

• 密文块要依赖以前的操作结果,所以，密文块不能进行重新排列;

• 可以使用不同的初始化向量来避免相同的明文产生相同的密文,一定程度上抵抗字典攻击;

• 一个错误发生以后,当前和以后的密文都会被影响;

CFB-加密反馈模式

加密反馈模式克服了需要等待8个字节才能加密的缺点，它采用了分组密码作为流密码的密钥流生成器；

定义：

​ Enc(X,Y)是加密函数

​ Dec(X,Y)是解密函数

​ Key是加密密钥；

​ Pi ( i = 0,1…n)是明文块，大小为64bit；

​ Ci ( i = 0,1…n)是密文块，大小为64bit;

​ Si ( i = 0,1…n)，大小为8bit，n个连续的Si组成加密位移寄存器，一般n=8;

​ Oi = Enc(Key, Si);

​ Lef(x) 为取数据x的最左8个bit位；

​ A(x,y)为合并x左移8位，空位用y填充

CFB加密算法可表示为：

​ S0 = IV；

​ Oi = Enc(Key, Si);

​ Ci = XOR( Ci, Lef(Oi));

​ Si = A(Si-1, Ci);

CFB解密算法可表示为：

​ S0 = IV；

​ Oi = Enc(Key, Si);

​ Ci = XOR( Ci, Lef(Oi));

​ Si = A(Si-1, Ci);

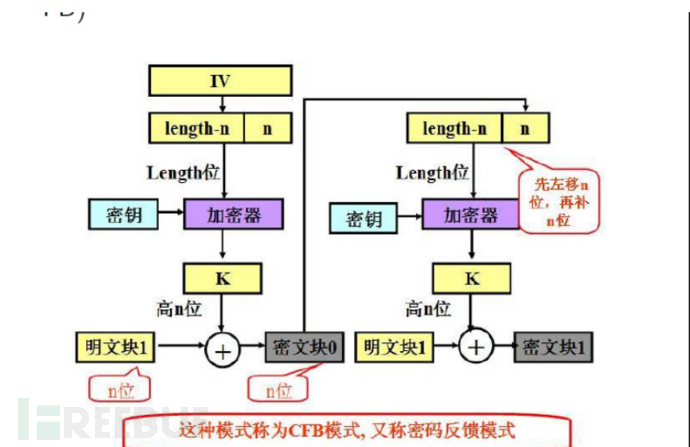
特点:

• 每次加密的Pi和Ci不大于64位;

• 加密算法和解密算法相同，不能适用于公钥算法；

• 使用相同的密钥和初始向量的时候，相同明文使用CFB模式加密输出相同的密文;

• 可以使用不同的初始化变量使相同的明文产生不同的密文，防止字典攻击;

• 加密强度依赖于密钥长度;

• 加密块长度过小时,会增加循环的数量,导致开销增加;

• 加密块长度应时8位的整数倍(即字节为单位);

• 一旦某位数据出错,会影响目前和其后8个块的数据;

OFB-输出反馈模式

与CFB模式不同之处在于, 加密位移寄存器与密文无关了,仅与加密key和加密算法有关；

做法是不再把密文输入到加密移位寄存器，而是把输出的分组密文（Oi）输入到一位寄存器；

定义：

​ Enc(X,Y)是加密函数

​ Dec(X,Y)是解密函数

​ Key是加密密钥；

​ Pi ( i = 0,1…n)是明文块，大小为64bit；

​ Ci ( i = 0,1…n)是密文块，大小为64bit;

​ Si ( i = 0,1…n)，大小为8bit，n个连续的Si组成加密位移寄存器，一般n=8;

​ Oi = Enc(Key, Si);

​ Lef(x) 为取数据x的最左8个bit位；

​ A(x,y)为合并x左移8位，空位用y填充

CFB加密算法可表示为：

​ S0 = IV；

​ Oi = Enc(Key, Si);

​ Ci = XOR( Ci, Lef(Oi));

​ Si = A(Si-1, Oi); 注意这里与CFB模式的不同

CFB解密算法可表示为：

​ S0 = IV；

​ Oi = Enc(Key, Si);

​ Ci = XOR( Ci, Lef(Oi));

​ Si = A(Si-1, Oi);

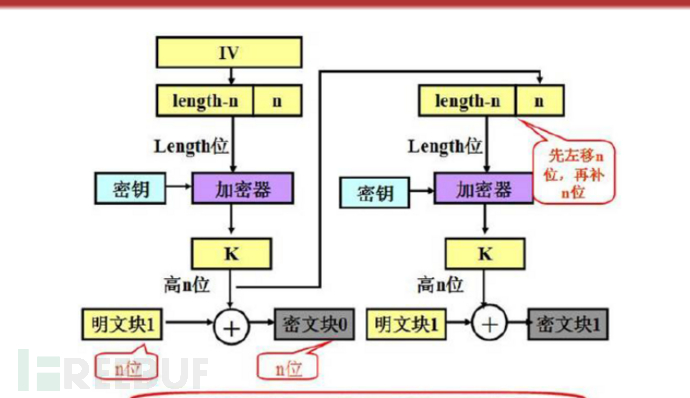
特点:

• 与CFB类似,以下都是不同之处;

• 因为密文没有参与链操作，所以使得OFB模式更容易受到攻击；

• 不会进行错误传播，某位密文发生错误，只会影响该位对应的明文，而不会影响别的位；

• 不是自同步的，如果加密和解密两个操作失去同步，那么系统需要重新初始化；

• 每次重新同步时，应使用不同的初始向量。可以避免产生相同的比特流，避免”已知明文”攻击 ；

CTR-计算器模式

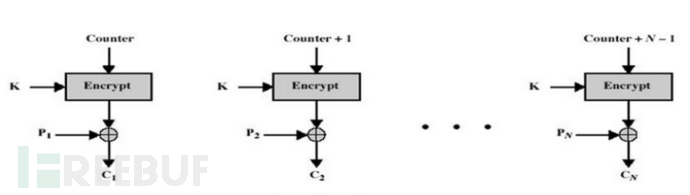
​ 计算器模式不常见，在CTR模式中， 有一个自增的算子，这个算子用密钥加密之后的输出和明文异或的结果得到密文，相当于一次一密。这种加密方式简单快速，安全可靠，而且可以并行加密，但是在计算器不能维持很长的情况下，密钥只能使用一次。CTR的示意图如下所示：

后记

参考文章

https://xuanxuanblingbling.github.io/ctf/crypto/2019/12/13/crypt/

https://hackmd.io/@amyriad/acsc#Wonderful-Hash-crypto-Score-340-11-Solves

https://blog.csdn.net/xiao__1bai/article/details/125262252

https://xz.aliyun.com/t/4069#toc-0

https://blog.csdn.net/jdhellfire/article/details/79680456

https://www.cnblogs.com/azbane/p/10179279.html

http://www.wjhsh.net/slqt-p-6559828.html

https://www.cnblogs.com/starwolf/p/3365834.html