一、序言

本篇为今年初发表的《DevSecOps建设之白盒篇》的续篇，在上一篇中，侧重讲了代码安全检测的自动化流程建设，对于白盒引擎技术的实现方面只是提了一下，还没有很详细的讲解，没有形成很完整的知识体系，所以有了本篇续文。

在文章的开头，我想先以一个使用者的角度来说说我对一款代码安全分析引擎的诉求：第一点，它的规则编写要简单易上手，且维护方便；第二点，它的CI/CD流程嵌入要友好；第三点、要支持人工辅助审计;第四点，它的数据分析价值要大；第五点、分析要准确；第六点、方便团队快速协作开发。

那么从第一点讲起，要求规则编写简单易上手，且维护方便，那么，就要求规则的添加尽量能以参数的形式进行，如果涉及逻辑处理，那么尽量能够以简单的脚本语言的形式进行。

第二点，要求流程嵌入要友好，那么就要求它以非编译的方式进行源码分析，且分析速度要尽可能的快。

第三点，要支持人工辅助审计，即引擎不仅仅是自动化进行审计的，审计结束之后，还支持加载人工的规则逻辑，进行二次审计，这样能够方便红队的同事进行漏洞代码审计和漏洞挖掘；

第四点，作为一个代码抽象数据库，那么其潜在的数据分析价值一定是很大的，那么就要求代码抽象数据库中存储的数据要尽量的全；

第五点，分析要准确，就要求，引擎需要建立起完整的数据流图，并能够将数据流路径作为重要依据，参与到漏洞的判定中。

第六点、方便团队快速协作开发，那么就要求使用的编程语言必须是这个方向领域最常用的语言，并且保持较低的代码耦合性。

针对以上的这些作为使用者的诉求，我们不妨来探索一款既能够满足企业内部自动化审计需求、又能够辅助白帽子日常快速挖掘漏洞的工具。那么，我觉得，这款代码安全分析引擎最好就是用python编写的，规则也支持python编写。下文提到的Aurora，即为笔者用python实现的一款代码安全分析引擎。当然，也不全是python，ast提取是用java写的(可忽略不计)，源码数据分析是用python写的。

那么，话说回来了，我们要如何准确的分析源码中的风险问题呢？我觉得最可靠的依据就是完整的数据流路径。我们知道，sink点代表漏洞点，source点代表可控入口点，如果具备从source点到sink的数据流路径，那么我们就有理由判定该处是存在安全风险的。

那么如何获取完整的数据流路径呢？这需要完整的数据流图，并根据图查询算法，查询出sink点及source点之间的路径。那么如何构建完整的数据流图呢？这是个难题，也是今天我们重点讨论的问题。

在此之前，我们先聊一下代码属性图这个东西。代码属性图，我最早是从Fabian Yamaguchi开源的一个叫joern的代码安全分析项目中了解到的。该项目将代码进行抽象化处理，并以图的形式进行表示。分析人员可将生成的代码属性图转存到诸如janusgraph，neo4j，orientdb等图数据库，并使用gremlin图查询语言进行漏洞分析。

这是一种非常巧妙的方案，但实际操作起来又有点局限性，首先要适应大规模的作业量，那么图数据库必须以集群形式给到，集群访问涉及网络请求，如果频繁请求资源又可能触发某些限制策略，如果网络延迟，那么程序分析的速度就会大大拖慢。

另外，个人感觉gremlin这类的图查询语言自由度不够高，写起规则来不太顺手。近几年倒是出现了一款非常不错的代码安全分析软件，叫codeql。codeql自身提供了一个图查询语言，并提供了非常友好的规则编写插件，从整体的方案上来说，和joern有点类似。

在实际的使用上，codeql的效果受到广泛的业内人士称道，成为目前主流的一款代码漏洞挖掘工具。但是话说回来了，真要集成到CI/CD中，编译问题可能又会成为它的一个阻碍。

下文实现的aurora代码安全分析系统可能和基于代码属性图的方式有点区别，主要区别是，数据不是存储到图数据库中的，而是存储到一个大字典中，这个字典的数据结构大致如下所示：

global_context={
  
  "job":{
      "job_id":"392302902332",
      "author_name":"pony",
      "project_name":"",
      "git_addr":"http://xxx",
      "branch_name":"xxx",
      "commit_id":"xxx",
      "start_time":"2021-12-31 00:00:00",
      "end_time":"2021-12-31 00:00:00",
    },
  "files":{
       file_id:{
         "file_name":"main.java",# 源代码名称
         "file_path":[path2file],# 源代码路径
         "source_file":""# 如果不允许收集代码，可缺。
               "job_id":""
       },
    },
  "classes":{
      "class_id":{
        "class_name":"",
        "package_name":"",
        "file_id":"32224423"
      }
    }
  "fields":{
      "field_id":{}#略
    },
  "methods":{
      # 函数摘要信息
      method_id:{
            "method_id": "",
            "method_name":"",# 函数名
            "class_name":"", # 类名
            "package_name":"",# 包名
            "root_id": "",  # 默认第一个节点为root节点
            "ast_nodes": { # ast节点,
                                      ast_node_id1:{},
                                                  ast_node_id2:{}
                                    },
            "is_dfa_analyzed": False,判断是否进行了数据流分析
            "CFG": {
                "block_nodes": {},  # block节点信息,
                "block_contains": {},# 包含了哪些表达式
                                                                "cfg_edges":{}, # 保存控制流关系
            },
            "dominant_tree": {},  # 支配树的信息,以直接支配关系存储
            "dominant_frontier": {},  # 支配边界信息
            "call_graph": {},  # 控制流图信息
            "DFG": {
                'dfg_node': {},# 数据流图节点
                'def_use_edges': {},# 基于SSA形式构建的def-use边关系
                "pass_through_edges": []  # 基于程序数据流流转规则添加的数据流边关系
            }
        }
    },

   "components":{
      # 程序中用到的组件信息，用以进行组件安全分析
    },
    
   "results": {
        # 漏洞分析结果
        "reports": {
             "xss":[
                                              {
                    "stainchain":"",#污点传播路径
                    "sink":"",#漏洞发生点
                    "stain":"",#污点
                    "flawsname":"",#漏洞名称
                    "description":"390390339",#漏洞描述信息，放description编号，到时候展示的时候通过编号从风险描述字典里索引。
                    'level':"5"#漏洞等级
                })
                                                 ]
        },
        "flaws_num": 0,
    }
}

其实这个大字典就是就是aurora的代码抽象数据库，基于这个大字典，也很容易生成代码属性图形式的数据库。而在实际分析过程中，aurora也会生成部分的代码属性图，并基于代码属性图进行数据流分析、污点追踪。aurora的代码属性图中，callgraph、cfg、dfg以及dominantTree都是在各自独立图中，这样我们就可以通过简单的图查询算法查询两个节点之间的路径。

下面我从解释这个代码数据的结构图，来带领大家了解Aurora静态代码分析引擎的实现原理。以上的代码抽象数据库主要包含以下几个部分：

components
methods
job
fields
classes
files
results

其中components部分存放的组件依赖信息，即maven或gradle项目的配置文件中提取的一些组件依赖信息。methods部分存放的是最重要的抽象数据，包括函数名，函数所属的scope，函数内各个block节点、表达式节点和数据流节点，以及各个各个block节点之间的控制流边关系和各数据流节点之间的数据流边关系。而数据流边关系中，又包含两部分的边关系来源，一部分是来自于def-use分析生成的数据流边关系，另一部分是来自于数据流路径流转规则分析生成的数据流边关系。而def-use边关系的生成又依赖于SSA形式的数据流分析方案。要生成源代码的SSA 表示形式，需要基于生成的控制流图，生成支配树，并且基于支配树生成，然后基于支配树，计算支配边界集合，继而基于支配边界集合，计算phi函数的放置位置。然后再基于支配树构造相关的算法进行变量rename。rename完之后即可遍历控制流图生成def-use链关系了。基于SSA生成的def-use链比传统数据流分析方案生成的def-use链简单且容易维护。job部分存放的是该作业的一些相关信息，包括目标项目的地址、分支及提交编号信息等。fields中包含所有类中的字段信息。files总包含所有的文件信息。classes中包含所有的类信息。results中包含分析结果信息。

二、控制流图构建

有了上述最基本的了解之后，下面我们来详细地讲一讲如何进行一款白盒引擎的开发。首先第一步是控制流的构建，而构建控制流最重要的一个环节就是基本块的划分。

要进行基本块划分处理，首先，我们可以通过javaparser-core这个库来看看java的语句结构包括哪些。在javaparser中，定义了15种Declaration结构，23种statement结构，35种expression结构，分别是：

声明语句

AnnotationDeclaration
AnnotationMemberDeclaration
BodyDeclaration
CallableDeclaration
ClassOrInterfaceDeclaration
ConstructorDeclaration
EnumConstantDeclaration
EnumDeclaration
FieldDeclaration
InitializerDeclaration
MethodDeclaration
Parameter
ReceiverParameter
TypeDeclaration
VariableDeclarator

表达式

ArrayCreationExpr
DoubleLiteralExpr
SuperExpr
BinaryExpr
UnaryExpr
AnnotationExpr
EnclosedExpr
SingleMemberAnnotationExpr
FieldAccessExpr
ArrayInitializerExpr
ArrayAccessExpr
NullLiteralExpr
ConditionalExpr
InstanceOfExpr
TypeExpr
CastExpr
AssignExpr
ThisExpr
MethodReferenceExpr
ClassExpr
ObjectCreationExpr
BooleanLiteralExpr
CharLiteralExpr
MemberValuePair
MethodCallExpr
VariableDeclarationExpr
NameExpr
NormalAnnotationExpr
StringLiteralExpr
LongLiteralExpr
MarkerAnnotationExpr
LiteralStringValueExpr
LiteralExpr
LambdaExpr
IntegerLiteralExpr

语句结构

WhileStmt
UnparsableStmt
TryStmt
ThrowStmt
SynchronizedStmt
SwitchStmt
SwitchEntryStmt
Statement
ReturnStmt
LocalClassDeclarationStmt
LabeledStmt
IfStmt
ForStmt
ForeachStmt
ExpressionStmt
ExplicitConstructorInvocationStmt
EmptyStmt
DoStmt
ContinueStmt
CatchClause
BreakStmt
BlockStmt
AssertStmt

这么多语法结构，可想而知，要构建一个完整的控制流结构所花费的精力有多大。但各位也不要太恐惧，这么多语法结构，其实归纳起来主要分为三种类型，即简单语句、复合语句、转移语句。

简单语句包括变量声明，赋值操作，函数调用等，这些语句都是表达式语句，由这些语句组成的线形语句串可直接合并为一个基本块。复合语句包括if语句、for语句、while语句、switch语句等，这是控制流构建算法的重点。其中，if语句和switch为控制流贡献分支。针对if语句，我们举一个例子。如：

int a=1;
if(x>1){
    a=a+1;
}
else if(x<1){
    a=a-1;
}
else{
    a=0;
}
System.out.println(a);

通过分析上面的代码，我们可以很容易将上述的代码划分为五个基本块即：

int a=1;  ->B1
a=a+1;    ->B2
a=a-1;    ->B3
a=0;      ->B4
System.out.println(a); ->B5

对应生成的控制流图如下所示

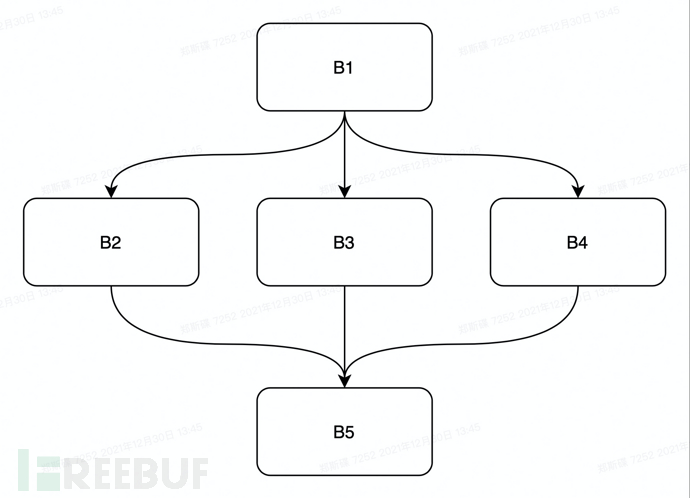
如图所示，从基本块B1伸出三个分支，对应if中的三个条件分支，最终三个分支聚合到基本块节点B5。其他语句可按照自己的理解进行代码块分割。

三、过程内数据流图构建

有了控制流图还不够，要判定漏洞是否存在，减少误报率，污点跟踪是必不可少的，而做污点跟踪，就得建立起完整的数据流图。下面我们来讨论下过程内数据流图怎么构建。这里通过综合考虑，我们采用了静态单赋值(SSA)方案来分析程序的数据流关系。

SSA form是一种源代码的中间表示形式，通过将源代码转为SSA形式，可非常方便且快速的进行数据流分析。将源代码转为SSA form主要分五个步骤，第一步是构建过程内完整的控制流图，第二步是生成过程内的支配树，第三步是生成支配边界，第四步是phi函数放置，第五步是变量重命名。

首先我们来讲一讲支配树的概念。不过咋一提出支配树的概念，可能很多人都一脸懵逼，下面我先科普一下支配关系相关的知识点。

第一，什么是支配关系？

在一个图里面，有两个点u和w，如果从图的源顶点出发，必须经过u才能到达w，那么我们称u支配w。

以下图为例：

那么根据支配关系的定义该控制流图中的支配关系如下：

1支配2，1支配3，1支配4，1支配5
2支配3，2支配4，2支配5

第二，什么是直接支配关系

如果u支配w，而w的其他支配者支配u，则节点u被认为是节点w的直接支配者，表示为idom (w)。

我们还是以上文中的控制流图为例，那么该控制流图中的直接支配关系为：

1直接支配2
2直接支配3，2直接支配4，2直接支配5

理解了以上两个定义，那么我们不难得出支配树的定义：

给定一个有向图，给定起点S，终点T，要求在所有从S到T的路径中，必须经过的点有哪些(即各条路径上点集的交集），称为支配点。简而言之，如果删去某个点（即支配点），则不存在一条路径能够使S到达T。由支配点构成的树叫做支配树。支配树上的两个相邻的点之间都是直接支配关系。所以我们不难得出该过程内的支配树如下：

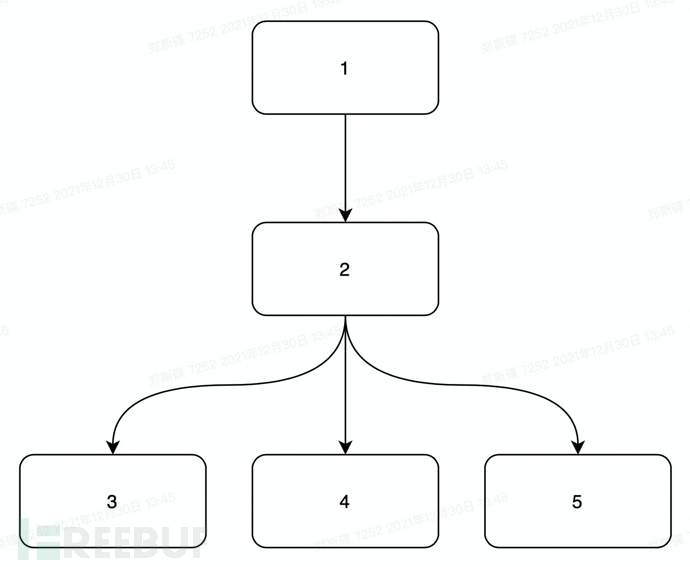
根据支配树的定义我们很容易的画出支配树，那么如何通过算法生成呢？可参考以下暴力算法生成：

def ssa_dfn_compute(rootid:str,successors:dict) -> list:
    '''
    @rootid       id of root node.
    @successors   the successors of target.
    计算dfn
    递归实现深度优先遍历
    '''
    def dfs(nodeid,nodelist):
        nodelist.append(nodeid)
        nexts=successors.get(nodeid)
        if nexts:
            for next in nexts:
                if next not in nodelist:
                    dfs(next,nodelist)
    nodelist=[]
    dfs(rootid,nodelist)
    return nodelist
    
def dominant_tree_build(rootid:str,successors: dict) -> dict:
    '''
    @rootid       the rootid of the cpg.
    @successors   cfg edges {"node1":[node2,node3,...]}

    @description:支配树构造，用于SSA中的变量rename，以及phi函数放置。
    可以利用edges {(idom(w),w)}生成。idom指w的直接支配节点。
    暴力构建支配树算法
    1.先对有向图进行dfs遍历，得到dfn序。
    2.然后针对dfn序中的每一个节点p，从节点开始重新遍历，到这个节点停止。
    3.然后再对dfn序进行遍历，没有被访问过的节点c都将父节点标记为节点p。
    '''
    # 求dfn序列
    dfn=ssa_dfn_compute(rootid=rootid,successors=successors) # 控制流图深度优先遍历序列

    def isVisited(nodeid: str,visited_node_list: list) -> bool:
        # 判断节点是否被访问过
        if nodeid in visited_node_list:
            return True
        else:
            return False

    def dfs(nodeid: str,visited_node_list: list):
        # @nodeid              the node waiting to visit.
        # @visited_node_list   the node which has already visited.
        # 深度优先遍历
        # 对控制流图从root节点开始进行深度优先遍历，直到遍历到输入的parent节点。
        if not isVisited(nodeid=nodeid,visited_node_list=visited_node_list):
            visited_node_list.append(nodeid)
            nexts=successors.get(nodeid)
            if nexts:
                for next in nexts:
                    if not isVisited(next,visited_node_list):
                        dfs(nodeid=next,visited_node_list=visited_node_list)

    dominant_tree={} # 支配树简单字典(类似邻接表表示法)
    # dominant_tree 中保存的是所有的被直接支配者与直接支配者之间的关系，dominant_tree[id]=dominant。
    for parent in dfn: # 遍历dfn序列
        visited_node_list = []
        visited_node_list.append(parent)
        dfs(rootid,visited_node_list)
        # 遍历dfn序列，将未遍历到的节点的支配节点都指向parent。后面在遍历后续的节点的时候会覆盖掉支配节点。
        for child in dfn: 
            if not isVisited(nodeid=child,visited_node_list=visited_node_list:
                dominant_tree[child] =parent
    return dominant_tree

上图为python实现的暴力生成支配树的算法，算法中已有非常详尽的注释，这里就不再赘述。

那么支配树有什么用呢？主要为第三步的支配边界集合构造和第四步的phi函数放置服务。

这里关于支配边界和phi函数，想必各位又有点懵逼了。所以在开展后续的讲解之前，我再来科普一下二者的概念。所谓的支配边界，学术上的定义是：A 支配 B 的一个前驱但不严格支配 B，则称 B 为 A 的支配边界。A 的所有支配边界组成的集合记为 DF(A)。DF 即 dominace frontier。（严格支配的定义是：如果x支配y，且x不等于y，那么说x节点严格支配y。）而计算支配边界的目的就是为了计算phi函数放置位置。

那么phi函数做什么用的呢？phi函数一般是放置在路径的聚合点，起到聚合所有达到的变量版本并对变量版本进行选择的作用。这是静态单赋值在分支上处理数据流传递关系的关键步骤。在聚合点后续的代码逻辑中，不用担心变量使用来自哪一个分支重定义的变量版本，在phi函数表达式中会重新定义一个变量版本，而后续的def-use链构建又可以直接通过查找相同变量名的形式查找目标def的use合集了。如下即支配边界合集的计算算法：

class SSADFCompute:
    '''
    处理支配边界集合求解
    '''
    @staticmethod
    def fetch_idom_from_dftree(dominant_tree:dict, nodeid:str) -> str:
        '''
        @dominant_tree  edges{idom}.
        @nodeid         target block node.
        @description:   fetch idom rel from dominance tree.
        '''
        return dominant_tree.get(nodeid) if dominant_tree else None
    
    @staticmethod
    def ssa_df_compute(precursors: dict,dominant_tree: dict) -> dict:
        '''
        @precursors     the precursors of target node.
        @dominant_tree  edges{idom}.
        支配边界计算目的
        - 定位需要插入phi节点的地方
        支配边界计算步骤
        - 找到控制流中的连接点block(多个前驱)
        - 为每一个连接点的block计算支配边界集合，其他的block节点自然也会在遍历过程中一起计算了。
        - 每一个block的支配边界集合用df(ni)表示
        - 一个高效的求解支配边界集合的方式是：先找到某个连接节点b2的前驱节点b1(排除掉它的直接支配节点)，然后在支配树上，从
        b1向上遍历到它的直接支配节点。然后将b2加入到遍历到的节点中。这样，遍历完所有连接点之后，所有的节点的支配边界结合即求解完毕。
        支配边界计算要点：
        - 遍历该节点的所有除了直接支配节点的前驱。
        df 算法参考Keith D.Cooper的论文《A Simple, Fast Dominance Algorithm》
        算法伪代码：
        for all nodes,b
            if the number of predecessors of b>=2
                for all predecessors,p,of b
                    runner <- p
                    while runner!=doms[b]
                     add b to runner's dominance frontier set
                     runner=doms[runner]
        算法要点提取：
        1、遍历所有节点，找到有多个前驱的节点。
        2、对这些节点进行向上遍历，直到节点的直接支配节点(不包括直接支配节点)。
        '''
        df_dict={}
        def recursion_up(idom: str,precursor: list,xnodeid: str):
            '''
            @xnodeid    带有两个前驱的连接节点
            @precursor  节点的前驱节点集合
            @idom       直接支配节点
            @description
             - 递归向上直到支配节点
             - 将节点添加到遍历到的节点的支配边界集合中
            '''

            for parent in precursor:
                if parent!=idom:
                    if not df_dict.get(parent):
                        df_dict[parent]=[]
                    if xnodeid not in df_dict[parent]:
                        df_dict[parent].append(xnodeid) # 将支配边界加入到遍历到的节点中
                    pre=precursors.get(parent)
                    recursion_up(idom=idom,precursor=pre,xnodeid=xnodeid)
                else:
                    break

        for nodeid,precursor in precursors.items():
            if precursor:
                if len(precursor)>1:
                    # 获取直接支配节点
                    idom=SSADFCompute.fetch_idom_from_dftree(dominant_tree=dominant_tree,nodeid=nodeid)
                    # 递归向上遍历直到直接支配节点
                    recursion_up(idom=idom,precursor=precursor,xnodeid=nodeid)
        return df_dict

在代码中已有非常详细的注释，这里我简要的说明一下算法的逻辑。首先获得以指向前驱节点形式存在的cfg关系合集precursors，遍历这个precursors，如果发现某个节点拥有两个及以上的前驱节点，则认为该节点处存在一个路径聚合点。

然后在控制流图上执行对该节点的递归向上的遍历，知道节点的直接支配节点，然后将该节点放置到遍历过程中经过的节点的支配边界中。

我们以上文中的if语句代码为例，在其控制流图中插入phi函数即得下图：

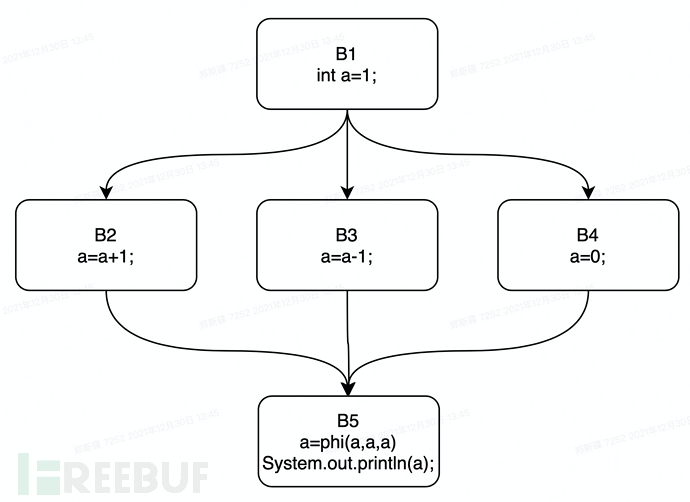
根据支配边界的定义，我们易知，节点B5是B2,B3,B4的支配边界，所以应在此处插入一个phi函数，用于处理此处聚合的多个分支的静态单赋值操作。根据支配边界和phi函数的定义，我们可以很容易在图中标出phi函数应该放置的位置，那么，如何用算法来实现这一过程呢？可参考如下伪代码实现：

function Place-phi-function(v) // v is a variable 
    //针对每一个控制流图中的变量，执行该函数进行phi函数的放置
    // has-phi(B, v)=true 表示变量v的一个φ-function已经放置在block B。
    // processed(B)=true  表示变量v在B上已经被处理了一次。 
    for all nodes B in the flow graph do
        has-phi(B, v) = false; processed(B) = false; 
    end for 
    W = ∅; // W 是一个工作队列
    // Assignment-nodes(v) assignmnet-nodes(v)表示一个带有v的赋值语句的节点集合。 
    for all nodes B ∈ Assignment-nodes(v) do
        processed(B) = true; Add(W, B); 
    end for
    while W != ∅ do
    begin
        B = Remove(W); 
        for all nodes y ∈ DF(B) do
           if (not has-phi(y, v)) then //如果变量v在y上未放置phi函数则
           begin
               place < v = φ(v, v, ..., v) > in y; # 将phi函数放在blocky中
               has-phi(y, v) = true; 
               if (not processed(y)) then # 如果基本块y未进行处理过，则处理y
               begin processed(y) = true; 
                   Add(W, y); 
               end 
          end 
        end for 
    end 
end

下面简要的解释下上述代码的逻辑。针对每一个控制流图中的变量，执行Place-phi-function。在Place-phi-function函数逻辑中，针对每一个控制流图中的节点，进行状态的初始化。

分别要设置是否存在phi函数(通过has-phi(B,v)函数来设置)，而函数processed(B)则是用来判断某个节点是否已经被分析处理过。然后遍历流图中所有的赋值语句集合，将包含复制语句的节点压入栈中进行处理，接着针对基本块B的所有支配边界，执行目标变量的phi函数添加工作。

这里由于还没有进行变量的rename，所以目前暂时不知道phi函数中的参数是来自哪个分支。那么如何对表达式中的变量进行重命名呢？可参考如下伪代码执行rename操作：

function Rename-variables(x, B) // x是变量，B是基本块
begin 
    ve = Top(V); // V 是x的版本栈
    for all statements s ∈ B do 
        if s is a non-φ statement then //如果是s是未插入phi函数的语句(非赋值语句)
            replace all uses of x in the RHS(s) with Top(V); 
            //将语句右侧x的所有使用用版本栈顶的那个元素进行替换。
        if s defines x then 
        begin 
            将变量x用新定义的版本名xv进行替换，并将xv压入版本栈。
            v = v + 1; // v 是版本号计数器
        end 
    end for
    for all successors s of B in the flow graph do //对所有B的后继节点执行
        j = predecessor index of B with respect to s 
        for all φ-functions f in s which define x do 
            replace the jth operand of f with Top(V); 
            //将phi函数中的参数用Top(V)中的变量版本进行替换
        end for 
    end for 
    for all children c of B in the dominator tree do 
        Rename-variables(x, c); 
    end for 
    repeat Pop(V); until (Top(V) == ve); 
end 
begin // calling program 
    for all variables x in the flow graph do 
        V = ∅; v = 1; push 0 onto V; // end-of-stack marker 
        Rename-variables(x, Start); 
    end for 
end

简单的解释下上述变量重命名算法的逻辑。首先对所有的变量执行Rename-variables函数，进行变量rename操作。而在Rename-variables函数中，遍历基本块B中的所有语句，对语句的RHS进行rename操作，如果语句中重新定义了该变量，则将变量下标加1，并将变量压入到版本栈中。

然后针对节点B的后继节点中，如果包含了phi函数，则对phi函数表达式中的参数进行rename，如果phi函数表达式重新定义了该变量，则同样，将变量版本加1，并push到版本栈中。然后，对基本块节点B在支配树上的所有子节点同样通过Rename-variables(x, c)函数执行rename操作。自后执行Pop(v)操作，将栈恢复到上一个支配节点中。

上述的rename算法并没有很复杂，但是实际处理起来需要处理很多细节的东西，比如在rename RHS的时候，所给到的语句并非都是简单的赋值语句，可能这个赋值语句的RHS中嵌套了对象创建语句、和函数调用语句，并且函数参数还是Binary形式的。这就需要我们尽可能的考虑多种情况，递归解析处理相关的语句，对其中的变量use进行rename。

下面我们还是以上文中的if语句为例，对这个if语句的控制流图进行rename操作。我们将对该if语句代码的支配树执行一个从B1开始的深度优先遍历。遍历的顺序是：B1,B2,B3,B4,B5。

下面我们可分步骤对这一过程进行重现。

Rename step1

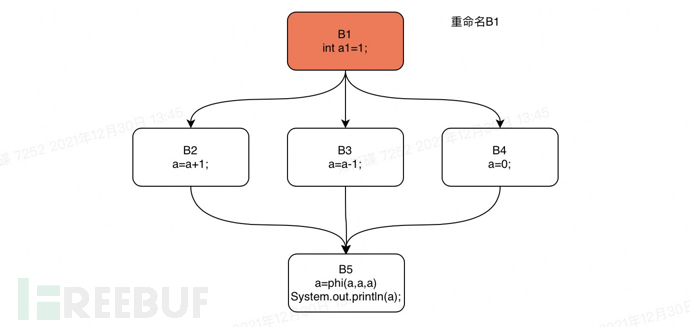
Rename step2

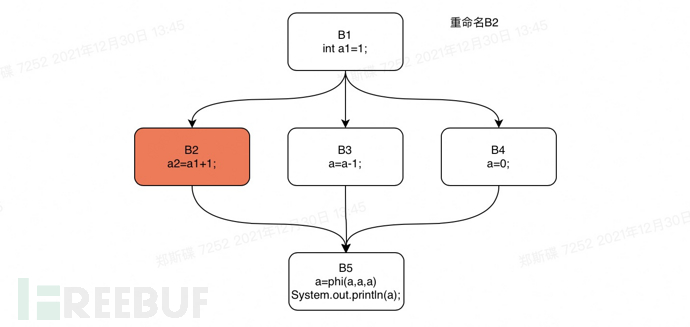
Rename step3

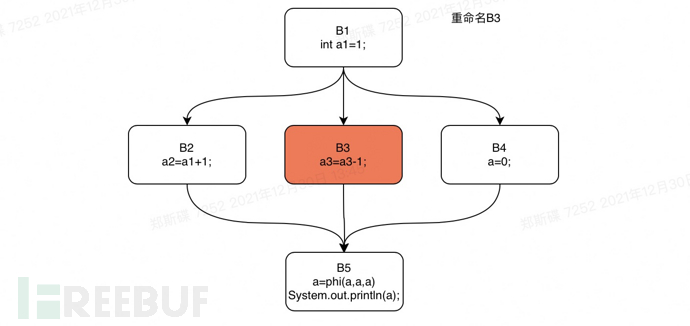
Rename step4

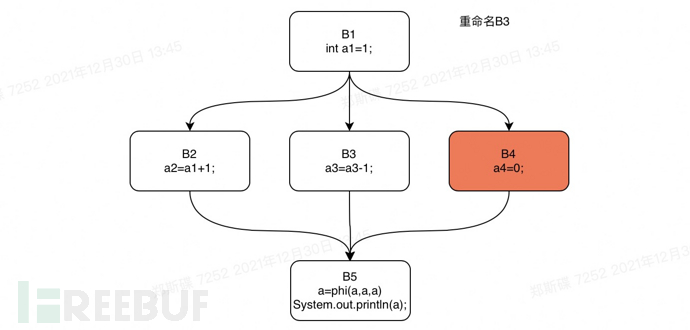
Rename step5

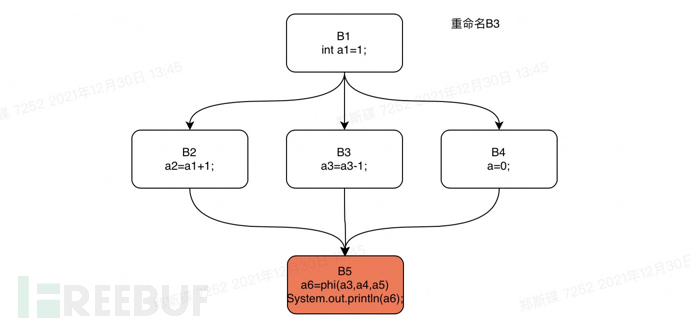
构建完毕源代码的SSA形式，下面我们就可以进行def-use链分析。基于SSA form分析生成的def-use链特别简单，因为每一个变量的use有且只有一个def，也就是说，只要遍历控制流图中的所有表达式节点，收集变量的def和use信息，然后将同名的变量def指向use即可。

四、全局污点分析

上文中讲解了如何基于SSA form生成过程内变量的def-use合集。但是光有def-use合集还不能够完整的描述数据在过程内的流动关系。因为def-use只解决了RHS中的变量use是由上面哪一个def来的，而没有解决LHS中的def是从哪里来的，它是否有和前面的数据流路径链接的可能。

首先，针对简单的binaryExpr及nameExpr，我们可以很容易通过赋值关系将RHS和LHS进行相连，从而将LHS中的def与前面的数据流连接起来，但是针对一些复杂的RHS我们就没办法轻易的将RHS和LHS进行。比如，RHS中是一个methodcallexpr,变量存在于methodcallexpr的参数中，这时候，我们能够说methodcallexpr中的参数一定会对LHS产生影响吗？不一定。

那么我们就需要有一个知识给到它，让它能够知道这个函数调用的某个位置的传参是会影响LHS的，从而建立LHS中的def与前面的数据流路径的关系。这一部分，据我调研，大部分厂商的做法基本都是通过补充数据流流转规则的形式，来补全这部分的数据流传播关系。在引擎研发的研发人员这边，可通过解析常见的java公共类库，来生成这部分的数据流流转规则，至于其他的第三方sdk中的库函数，则需由后续维护人员自行添加了。当然有人可能会问能不能够自动化生成？理论上是可以的，但是实际上分析引擎的执行效率会大大降低。

在补全了过程内的数据流传播后，我们还不能够准确的找到漏洞，因为很多情况下，source点和sink点是不在同一个函数中的，这就需要我们的引擎需要具备过程间分析的能力。过程间分析其实说来也简单，只需要建立函数调用处的实参和函数声明处的形参之间的联系即可，这样一来，两个过程的数据流图便连接了起来。但是，需要注意的是，这部分的联系需要建立在被调用的函数也被解析过的前提上。

那么，我们如何确保被调用的函数已经被解析过了呢？有两种方案，一种方案是在遇到函数调用的时候再解析，然后标注解析状态为true，另一种方案是直接将目标漏洞分析所需要的过程全部分析好，这就需要建立必要的函数调用图，然后遍历函数调用图进行过程分析。生成函数调用图的一个好处是，我们给定污点之后，就可以生成所有该污点可能达到的过程，这样可以在开始的时候就有一个全局的把握，后续进行sink点定位的时候，可以遍历这个调用图来查找，这样效率上会快很多。

在建立起了一个全局的数据流图之后，我们就可以遍历这个数据流图进行漏洞分析了。那么我们要如何进行遍历分析呢？如何标记污点和sink点呢？这里我们需要先定义好两种数据结构。一个是数据流节点，一个是ast节点。数据流节点的ast节点的具体结构就不再赘述，但是这其中必须要包含一个编码参数用于标识这个节点，这样我们才能够在全局唯一确认这个节点，避免在数据流遍历的时候错误遍历到了其他的同名节点上。数据流节点中包含的信息是比较少的，如果直接根据数据流节点的name来标记污点，那么准确度将大大降低。

有一种方案是在前期数据流分析的时候，可建立起数据流节点和ast节点之间的关联关系，然后在标记的时候，通过分析ast表达式节点，判断该ast节点是否存在污点，如果存在污点，则可将其对应的数据流节点标记为污点。当然也有另一种方案就是直接在数据流分析阶段，在处理函数调用的时候，就分析其是否为污点，如果是，则数据流节点上用一个istaint的属性标记。同样，如果是sink点的话，也可以用issink来标记。后续只需要查找数据流图中哪些是被标记为istaint的节点，哪些是issink的节点，然后通过图遍历算法，即分析得从污点到sink点之间是否存在数据流路径。

五、漏洞规则引擎

一个好的规则引擎可以让整个白盒引擎变得更加有活力。比如codeql，开放性的规则引擎，通过dsl查询语言，进行漏洞规则的编写，并且给予灵活的api调用，能够极大的将白帽子的知识赋能给引擎，从而让引擎发挥出更大的能力。虽然，codeql很强大，但是很多人还是觉得为了挖漏洞去熟悉一门在其他地方没啥应用场景的dsl语言有点太浪费时间，所以，在研发的初试，我就决定插件的脚本要是一门非常简单易上手的语言，即python，相信绝大部分做网络安全相关的人都会python吧？

下面是aurora的规则引擎(严重借鉴codeql的思路，哈哈哈)

'''
xss 漏洞检测规则
'''
from core.taintTrack.taintTracker import taintTracker
from core.dfa import dfa
from .base import base
class xss_rules(base):
    def __init__(self):
        self.name="xss"
        self.description="略"
        self.advise="略"
        self.level=5
        self.source_rule=[
            'getCookies', 'getRequestDispatcher', 'getRequestURI', 'getHeader', 'getHeaders',
            'getHeaderNames', 'getInputStream', 'getParameter', 'getParameterMap']
        self.sink_rule=["println"]
        self.clean=[]

        super().__init__(sink_rule=self.sink_rule,source_rule=self.source_rule,clean_rule=self.clean)
        # 数据流节点
        self.sources=[]
        self.sinks=[]
        self.config_source_node()
        self.config_sink_node()
        self.config_clean_node()

    def check(self,graph:dict,method_id_list:list,rule:dict):
        '''
        漏洞检测
        '''
        taint_tracker=taintTracker(graph=graph,method_id_list=method_id_list,rule=rule)
        taint_tracker.taintTrack()  # 污点追踪
        taint_tracker.get_results()  # 结果
        taint_tracker.env_clean()  # 清理环境

    def config_source_node(self):
        # 开始漏洞分析
        self.sources=self.search_source(
            global_context=dfa.DFGPathBuilder.global_context,
            source_rule=self.source_rule
        )

    def config_sink_node(self):
        '''
        查找sink点
        '''
        self.sinks=self.search_sink(
            global_context=dfa.DFGPathBuilder.global_context,
            sink_rule=self.sink_rule
        )

    def config_clean_node(self):
        dfa.DFGPathBuilder.global_context['clean_rules'] = self.clean

简单的说一下规则引擎的思路，config_source_node、config_sink_node及config_clean_node三个函数分别是用来配置污点、sink点、净化点的。search_source函数通过遍历函数调用图中的过程的表达式，找到其中的带有污点的表达式，然后在后续进行数据流分析构建的时候，对这个ast节点对应的数据流节点进行污点标记，sink点和clean点同样操作。使用者可以根据规则引擎提供的ast数据访问接口，添加更多的污点标记逻辑，这一部分也是有待后续探索的。

当然在一开始的时候，规则方面只打算做成配置的方式，因为觉得大部分的补充能力包括规则都可以通过配置的方式给到，比如fortify，大部分规则都是通过配置的形式。但是考虑通过脚本语言的形式编写漏洞检测插件，或许能够像codeql那样，能够更好地融合白帽子的知识力量。

个人觉得这个白盒引擎后期还挺有搞头，第一，不用编译，直接解析javaparser分析构建数据流图，第二，规则脚本使用python编写，对白帽子非常的友好。

六、关于开源

本篇主要是为了分享一下这一年在白盒研发方面的经验，能够让各位还在迷途中的同行有一个比较成系统性的理论参考，至于开源，目前还没有这个打算。但是过一阵，等引擎更加的完善，能够为这个社区作出一些贡献的时候，可能会考虑开源。

七、参考

https://groups.seas.harvard.edu/courses/cs252/2011sp/slides/Lec02-Dataflow.pdf

八、About me

747289639@qq.com(微信同)

By 郑斯碟

from 理想汽车安全部