上一篇椭圆曲线算法（ECC）学习（一）中我们讲述了椭圆曲线算法的基本数学常识和加密解密过程，作为椭圆曲线数学的一种公钥密码的算法，其优点毋庸置疑。区块链最近异常火热，那么今天我们就来讲讲区块链的关键加密技术，椭圆曲线secp256k1。

Secp256k1是指比特币中使用的ECDSA(椭圆曲线数字签名算法)曲线的参数，并且在高效密码学标准（Certicom Research，http://www.secg.org/sec2-v2.pdf）中进行了定义。

0x01 前言

Secp256k1为基于Fp有限域上的椭圆曲线，由于其特殊构造的特殊性，其优化后的实现比其他曲线性能上可以特高30％，有明显以下两个优点：

1）占用很少的带宽和存储资源，密钥的长度很短。

2）让所有的用户都可以使用同样的操作完成域运算。

0x02 正文

椭圆曲线数字签名算法(ECDSA)

用户的密钥对:

（ d, Q ）

待签名的信息： M

签名：

签名过程：

1）根据ECC算法随机生成一个密钥对

2）令

如果r = 0，则返回步骤1

3）计算 

4）按照数据类型转换规则，将H转化为一个big endian的整数e

5）

若s = 0, 则返回步骤1

6）输出的

即为签名。

验证过程：

1） 计算                                                                  

2）按照数据类型转换规则，将H转化为一个big endian的整数e
3）计算                                       

4）计算                                          

如果R = 零点，则验证该签名无效

5）令 

6）若 v == r，则签名有效，若 v ≠ r, 则签名无效。

0x01 Secp256k1椭圆曲线

Secp256k1椭圆曲线形如:

椭圆曲线域参数由单元T =（p，a，b，G，n，h）指定

• p = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
• = 

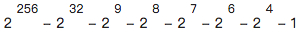
Fp上的曲线 E: 由下式定义： 

• a = 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
• b = 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000007

压缩形式的基点G是：

• G = 02 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798

而在未压缩的形式是：

• G= 04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8

最后，G的阶为： 

• n = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141

协因子：

h = 01

0x03 算法实现

在查阅资料时，发现了GitHub上的一个关于secp256k1的一个项目,这是一个针对曲线secp256k1上的EC操作优化的C库.

github地址：https://github.com/bitcoin-core/secp256k1

当然在steem-python也有相似的secp256k1-py库,运用pip安装secp256k1-py库、安装pkg-config

pip install --no-binary:all: secp256k1
sudo apt-get install libtool
sudo apt-get install autoconf
sudo apt-get install pkg-config

当准备工作做好后，我们就可以使用这个库

私钥公钥生成

python -m secp256k1 privkey -p

使用私钥对明文进行消息签名

python -m secp256k1 sign \
  -k c6e193266883a500c6e51a117e012d96ad113d5f21f42b28eb648be92a78f92f \
  -m hello

使用明文、公钥、签名，来检验是否是对应的私钥的所加密的

python -m secp256k1 checksig \
  -p 0314bf901a6640033ea07b39c6b3acb675fc0af6a6ab526f378216085a93e5c7a2 \
 
 -m hello \  -s 
3045022100a314a579fb9f30a804c172eec4881ed603e661eed692797149dfdbce24d671d202203ccfab0603ad97c34864caa22d42a24d0cb5750fcb159476b8ae30a11edc0ed6

0x04 总结

经过两期的介绍，希望大家理解这个复杂的非对称加密算法中的离散问题。为了保护储存在区块链中的信息的安全与完整，区块链就使用上述的包括另一种（哈希函数）的密码现代密码学技术。希望各路大牛多加指正在下面评论中

相关链接：

[1]  https://en.bitcoin.it/wiki/Secp256k1

[2]  区块链指南 机械工业出版社

[3]  Douglas R.Stinson. 密码学原理与实践（第三版）电子工业出版社 2009

[4]  https://en.bitcoin.it/wiki/Elliptic_Curve_Digital_Signature_Algorithm

[5]  Michael E.Whitman 信息安全原理（第五版） 清华大学出版社