零知识证明是一种可在多方交互验证需求中实现隐私保护的密码学方案，用于在不泄露具体数据的情况下对数据知识的掌握或相关计算的正确性进行证明，经过密码学学术界和金融科技等产业界多年的理论研究与实践检验，目前已在区块链等与数据隐私相关的创新业务场景实现了落地应用。

本文介绍了零知识证明的基本概念、研究进展、实现原理等情况，并对zk-SNARK等典型的通用零知识证明算法进行了分析，最后对零知识证明技术在区块链与数字货币、安全多方计算等领域的应用进行了梳理总结。

一、零知识证明概述

零知识证明（Zero-Knowledge Proof, ZKP）是现代密码学中的一类经典协议，用于在不泄露关于某个命题任何信息的情况下证明该命题的正确性。近年来，随着区块链等新兴技术的发展以及隐私计算需求的兴起，零知识证明技术再次成为包括金融科技、大数据等相关行业关注的焦点。

如图1所示为零知识证明的一个经典模型——洞穴模型[1]，该模型不涉及具体算法实现，仅用于初步说明零知识证明的原理和效果。

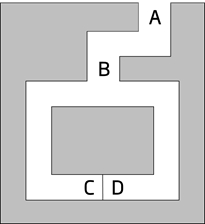
图1：洞穴模型

在图中，C点和D点之间存在一道密门，只有知道秘密口令的人才能打开。证明者（Prover）P知道秘密口令，并希望向验证者（Verifier）V证明，但又不希望泄露秘密口令，可通过以下证明过程实现：

①首先，验证者V站在A点，证明者P站在B点；

②证明者P随机选择走到C点或D点，验证者V在A点无法看到证明者P选择的方向；

③验证者V走到B点，并要求证明者P从左通道/右通道的方向出来；

④证明者P根据验证者V的要求从指定方向出来，如有必要需要用秘密口令打开密门。

如果证明者P知道秘密口令，就一定能正确地从验证者V要求的方向出来；如果证明者P不知道秘密口令，则每次有1/2的概率能从验证者V要求的方向出来。该证明过程可重复进行多次，直到验证者V相信证明者P拥有打开密门的秘密口令。

通过以上证明过程，证明者P就向验证者V完成了关于秘密口令的零知识证明，即证明过程不会泄露任何关于秘密口令的知识。

1、概念起源与发展

零知识证明的概念最早在20世纪80年代由美国麻省理工学院的Shafi Goldwasser、Silvio Micali和Charles Rackoff在论文《The Knowledge Complexity of Interactive Proof Systems（交互式证明系统中的知识复杂性）》（以下简记为GMR85）中提出[2]，该论文对交互式证明系统的零知识性进行了数学定义，并提出了一种关于二次剩余（Quadratic Residue）判定问题的零知识证明协议。二次剩余问题是数论中的经典问题，其内容是给定互素的整数a和n，判断a是否是模n的二次剩余。由于当n为合数时，不存在多项式时间的算法能够判定该问题，因此二次剩余问题是一个等价于整数分解问题的NP问题。GMR85论文提出的二次剩余问题证明协议可实现证明者向验证者证明a是模n的二次剩余，而验证者在相信该论断的同时无法获知x的具体值等除“a是模n的二次剩余”以外的任何信息。

GMR85等早期论文提出的方案大多数是专用的交互式零知识证明协议，仅能证明某一类特定的问题，且需要证明者和验证者进行多轮交互才能完成，其功能和实际应用效果难以满足现实应用场景的要求。为了能够实现针对任意问题的通用证明协议，同时避免多次交互给实际应用带来的局限性，非交互式通用证明协议的研究成为了零知识证明自概念诞生以来的重要发展方向。

目前，数据安全与隐私保护成为了区块链等应用中的重要需求，零知识证明这一经典的密码学算法有了新的应用前景。在区块链应用场景中，实现多参与方的频繁交互是不现实的，且复杂多样的业务模式催生了通用证明协议的应用需求。因此，zk-SNARK等非交互式通用零知识证明协议在区块链与数字货币等场景中得到了广泛的应用。

2、经典示例

为了能够更加清楚地说明零知识证明的概念，本小节用数独问题[3]和三色图问题[4]两个简单的示例进行具体阐述。

（1）数独问题

如图2所示的数独游戏盘面为由九个3×3区域（宫）组成的9×9九宫格，要求玩家在这个已经填有若干1~9数字（谜面）的9×9九宫格内继续填满数字（谜底），使得每一行、每一列、每一宫（3×3）内都包含不重复的1~9数字。

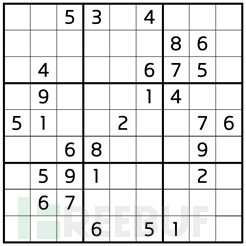
图2：数独游戏

证明者P希望向验证者V证明其知道某个数独游戏的解，但又不希望向验证者V泄露解的具体内容，可通过以下过程实现证明：

①证明者P将9组1~9数字写在81张卡片上，并在验证者V回避的情况下按照解的排列摆放好，谜面数字朝上，谜底数字朝下；

②验证者V随机选择按照每一行、每一列或每一宫进行验证；

③证明者P在验证者V的见证下，按照验证者V的要求将81张卡片以每一行/列/宫为一组放在9个不透明的袋子中，并打乱每个袋子中的卡片顺序，交给验证者V；

④验证者V打开9个袋子，如果每个袋子中均为9个1~9不重复的数字，则本次验证通过。

证明者P通过预先猜测验证者V会选择哪种验证方式（行/列/宫）进而成功欺骗验证者V的概率是1/3。因此，验证者V可以每次随机选择不同的验证方式将以上证明过程重复多次，直到验证者V相信证明者P知道该数独游戏的解，且验证者V在整个过程中并不能获知任何关于解的具体信息。

（2）三色图问题

三色图问题即用三种颜色对一个地图进行着色，使得任意两个相邻区域的颜色均不相同。三色图问题是一个NP完全问题，不存在多项式时间内的求解算法。根据图论原理，地图的着色问题可以等价于连通图的顶点着色问题。为了便于表示，以下用连通图的顶点着色进行问题说明，其证明过程如图3所示。

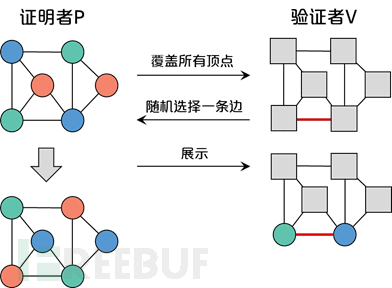
图3：三色问题证明过程

证明者P希望向验证者V证明其知道某个连通图的着色方案，但并不希望让验证者V获知这一方案的内容，其证明过程如下：

①证明者P根据其掌握的着色方案随机选择三种颜色对连通图的所有顶点进行对应着色，并将图中的每个顶点用纸片进行覆盖，展示给验证者V；

②验证者V可随机挑选连通图中的一条边进行验证；

③证明者P将这条边连接的两个顶点上覆盖的纸片揭开，展示给验证者V，如果这两个顶点颜色不同，则本次验证通过。

以上证明过程同样需要重复进行足够多次才能使验证者V相信证明者P掌握着色方案，且证明者P每次需要重新随机选择三种颜色对原有着色进行替换，否则验证者V可能根据验证结果还原出着色方案的部分内容。经过足够大的n次重复之后，证明者P在不掌握着色方案的情况下成功欺骗验证者V的概率是可忽略的，即验证者有足够的理由相信证明者P真正掌握了对应图的着色方案。

与本文最开始的零知识证明洞穴模型相比，以上两个零知识证明概念演示示例虽然更具有现实性，但仍然不是实用的零知识证明协议，也都需要证明者与验证者反复进行多次证明过程才能以较大的概率使得验证者信服。而在真实的零知识证明协议中，通过引入数学与密码学手段对方案进行约束，使得证明者每次都无法伪造证明，也就无需进行反复的证明和验证。

二、零知识证明技术原理

本章将对零知识证明的技术原理进行进一步分析，包括零知识证明在密码学上需要满足的基本属性，以及以经典的Schnorr协议为例说明交互式零知识证明协议到非交互零知识证明协议的转化。

1、基本属性

零知识证明涉及的密码学与数学理论较多，包括计算/统计不可区分性（Computationally/Statistically Indistinguishiable）、模拟器（Simulator）、随机预言机（Random Oracle）模型等计算复杂性理论内容。为了便于理解，我们将零知识证明协议的三个基本属性用较为通俗的语言描述如下：

①完备性（Completeness）：只要证明者P拥有相应正确知识，就能够通过验证者V的验证，即P有足够大的概率使V确信。

②可靠性（Soundness）：如果证明者P没有相应正确知识，则无法通过验证者V的验证，即P成功欺骗V的概率可忽略。

③零知识性（Zero-Knowledge）：证明者P在交互的过程中仅向验证者V揭露其是否拥有相应正确知识，而不会泄露任何关于知识的额外信息。

2、交互式零知识证明

零知识证明起源于交互式证明协议，本小节以Schnorr协议[5]为例分析交互式零知识证明的原理和特点。Schnorr协议是一种身份认证协议，也是如今许多数字签名方案（例如DSA算法和ECDSA算法）的基础，其简化的协议流程如图4所示。

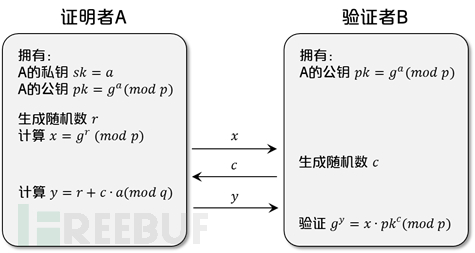
图4：简化Schnorr协议流程

在Schnorr协议中，证明者A通过和验证者B进行三次交互的方式证明了其拥有公钥pk对应的私钥sk，而验证者B无法在整个过程中获取私钥sk的信息。

3、非交互式零知识证明

交互式零知识证明协议依赖于验证者的随机尝试，需要证明者和验证者进行多次交互才能完成。非交互式零知识证明（Non-Interactive Zero-Knowledge, NIZK）[6]将交互次数减少到一次，可实现离线证明和公开验证。例如，在区块链等零知识证明应用场景中，通常需要将证明进行直接发布，而非依赖于交互实现，且需要支持多方的公开离线验证。因此，在实际应用中需要考虑如何实现交互式零知识证明协议的非交互化。

对于Schnorr这一具体协议而言，可通过基于随机预言机模型的Fiat-Shamir变换[7]将其转化为非交互式零知识证明，即Schnorr签名。Fiat-Shamir变换将交互式协议中验证者的每次随机数挑战行为用证明者执行随机预言机代替，随机预言机的输入应包含之前的所有上下文信息。随机预言机可以看作是一个理想化的哈希函数，能够将输入转化为具有真随机性（满足一致性分布）的结果。在实际应用中，由于不存在理想化的随机预言机，可以使用SHA-256等常用的密码学哈希算法进行实现。

即在基于Fiat-Shamir变换的非交互式Schnorr协议证明过程中，随机挑战数c不再由B生成并发送给A，而是由A自己通过c=H(x||M)计算挑战数c，其中H(∙)是哈希函数（随机预言机），M是任意消息串。最后A将(c, y)作为证明值进行发布，同时发布消息M。任何获知证明值(c, y)、消息M和公钥pk的验证者均可在与交互式协议相同的验证方式基础上进一步验证c=H(x||M)是否成立。

证明者A在没有交互的情况下得到了随机挑战数c，因此省去了交互式协议中验证者B随机选择c并发送给证明者A的交互过程。这一非交互式的Schnorr协议也被称为Schnorr签名机制，即证明者A使用自己的私钥sk=a对消息M进行了签名，其他人可通过A的公钥pk验证这一签名。

除了通过随机预言机模型将交互式协议转化为非交互式协议外，在后来的zk-SNARK等具有通用功能的零知识证明构造中，还可采用公共参考串（Common Reference String, CRS）的形式实现协议的非交互性，即在进行非交互式证明前由可信第三方生成一个可信的随机串，用于替代交互式证明过程中的随机挑战数。在Zcash等采用零知识证明技术的数字货币中，为了保证过程和结果的可信性，通常会基于一种称为可信设置（Trusted Setup）的仪式用于产生公共参考串。

三、零知识证明典型算法分析

为了能够使零知识证明在更多业务场景中应用，可实现通用功能的非交互式零知识证明算法具有更强的应用普适性。因此，本章选取zk-SNARK等在区块链等场景中应用较多的通用非交互式零知识证明算法进行分析。

1、zk-SNARK

zk-SNARK（Zero-Knowledge Succinct Non-interactive Arguments of Knowledge，零知识简明非交互式知识论证）是一类应用广泛的通用零知识证明方案，通过将任意的计算过程转化为若干门电路的形式，并利用多项式的一系列数学性质将门电路转化为多项式，进而生成非交互式的证明，可实现各类复杂的业务场景的应用。目前，zk-SNARK已在数字货币、区块链金融等区块链领域实际落地，是目前最为成熟的通用零知识证明方案之一。

（1）基本框架

从整体上而言，zk-SNARK零知识证明协议可大致分解为以下步骤：

①将计算转化为电路

首先，为了将待证明的计算式进行统一处理，需要将其转化为若干个门电路的组合形式。例如，证明者A希望向验证者B证明其知道使得计算式(c1×c2)×(c1+c3)=7成立的c1、c2、c3值，而不泄露c1、c2、c3的具体值。根据zk-SNARK协议，首先需要将计算式(c1×c2)×(c1+c3)=7转化成如图5所示的电路。

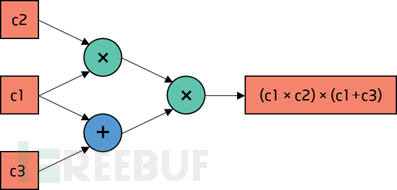
图5：电路示例

在进行程序表达时，还需要引入一些中间变量，即：

c_1 * c_2 = sym_1

(c_1 + c_3) * 1 = sym_2

sym_1 * sym_2 = out

其中，sym1和sym2为中间变量，out为公开的输出值，即7。

②将电路转化为R1CS

第二步是将表示计算式的电路转化为向量点积（内积）的形式，即一阶约束系统（Rank-1 Constraint System, R1CS）。对于每个门电路，需要定义一组向量(l, r, o)，通过向量内积运算使得s∙l×s∙r-s∙o=0，其中s代表全部输入组成的向量，即s=[one, c1, c2, c3, sym1, sym2, out]（元素排列没有固定顺序），one表示值为1的虚拟变量，用于将加法门电路c1+c3=sym2统一表达为(c1+c3)×1-sym2=0的形式。向量s在zk-SNARK中又被成为证据（Witness），作为证明者生成证明的输入参数。

对于乘法门电路c1×c2=sym1，对应的三个向量(l, r, o)分别为：

l=[0,1,0,0,0,0,0]

r=[0,0,1,0,0,0,0]

o=[0,0,0,0,1,0,0]

将s、l、r、o代入s∙l×s∙r-s∙o=0即得c1×c2-sym1=0，与门电路c1×c2=sym1等价。同理可得加法门电路c1+c3=sym2对应的向量为：

l=[1,0,0,0,0,0,0]

r=[0,1,0,1,0,0,0]

o=[0,0,0,0,0,1,0]

即1×(c1+c3)-sym1=0。最后一个乘法门sym1×sym2=out对应的向量为：

l=[0,0,0,0,1,0,0]

r=[0,0,0,0,0,1,0]

o=[0,0,0,0,0,0,1]

即sym1×sym2-out=0。通过以上过程，就将待证明计算式对应的电路编码成了R1CS向量的形式。

③QAP

第三步是将R1CS向量表达式转化为多项式的形式，即QAP（Quadratic Arithmetic Programs）。通过这一重要步骤，即可实现待证明计算式验证和多项式验证之间的等价转换。

具体而言，首先在有限域上选择三个不同的值，假设为1、2、3（在实际应用中需要随机选择），然后通过拉格朗日插值公式，构造三组多项式l(x)、r(x)、o(x)，使得在x的取值分别为之前选择的1、2、3时，多项式向量组(l(x), r(x), o(x))的三种取值分别对应第二步中三个门电路的向量组(l, r, o)的三种不同取值。取多项式P(x)=s∙l(x)×s∙r(x)-s∙o(x)，当x取值为1、2、3时，P(x)=0，即1、2、3为多项式P(x)的三个根，因此多项式P(x)能够被T(x)=(x-1)(x-2)(x-3)整除，即存在多项式H(x)使得P(x)=T(x)×H(x)。

上述QAP过程将证明原计算式转化成了证明存在多项式H(x)使得P(x)=T(x)×H(x)。通过拉格朗日插值公式引入了大量与原计算式无关的值将向量取值转化为多项式约束，因此多项式与原计算式在本质上并不完全等价，但根据多项式的Schwatz-Zippel定理，验证了转化后的多项式即相当于验证了原计算式。

④引入约束

以上步骤完成了计算式证明到多项式证明的转化。为了构造完整的零知识证明方案，需要再引入一系列约束方法构造完备的零知识证明协议。具体包括：

引入指数知识假设（Knowledge-of-Exponent Assumption, KEA）或椭圆曲线密码体系下的系数知识假设（Knowledge-of-Coefficient Assumption, KCA）约束证明者在生成证明过程中的参数使用，防止证明者通过选择不符合限制条件的多项式进行欺骗。

防止暴力破解：为了保证证明的零知识性，防止验证者在有限范围的多项式系数组合中对证明结果进行穷举破解，进而反推出证明者的原始多项式，需要生成一个秘密的随机数来对证明结果进一步的加密。

使用双线性配对实现验证过程中需要使用到的乘法同态。

为了实现非交互式零知识证明，需要事先由第三方生成一些秘密随机数，并进一步生成证明密钥（Proving Key）pk和验证密钥（Verification Key）vk，pk和vk将作为公共参考串CRS分别赋予证明者和验证者，而原始的随机数则作为“有害废料”（Toxic Waste）进行销毁。

（2）方案选择

zk-SNARK的概念最早于2011年提出[8]，其方案基于2010年提出的Gro10论文[9]。目前，zk-SNARK已有多类不同的优化方案，主流论文包括Pinocchio协议[10]、BCTV14a[11]、Groth16[12]等等。Pinocchio协议是首个完整的zk-SNARK实用方案，后续论文方案大多基于经典的Pinocchio协议进行优化，因此具有一定的代表性。在Pinocchio协议中，初始化过程、证明过程、验证过程分别由可信第三方、证明者、验证者执行。在业务模式（待证明计算式形式）确定后，可通过可信第三方或多方公开生成的可信方式产生公共参考串CRS，供后续的证明和验证使用。

由于存在着许多基于Pinocchio协议的不同优化方案，且相关学术论文仍在不断地更新之中，因此zk-SNARK的方案选择是一个值得考虑的问题。目前，现有的算法工具大多支持Groth16或BCTV14a方案。与BCTV14a方案相比，Groth16方案支持可证明安全，且在Zcash等数字货币应用中多以Groth16作为默认方案。因此，在进行实际应用时，可优先选择应用最为普遍的Groth16方案作为工程实现的基础。

（3）功能实现

除上述的(c1×c2)×(c1+c3)=7这类简单的计算式证明外，还可通过不同的电路构造方法，将更为复杂的证明需求转化为门电路的组合形式。libsnark算法库中的gadget工具库包含布尔值、位组合、析取关系（或）、合取关系（与）、大小关系、向量内积、线性组合等基本约束的实现，通过包括但不限于以上基本功能的组合，可实现更为复杂计算式的证明。除基本功能外，zk-SNARK还可实现Merkle树、SHA256哈希、模指数运算、双线性配对等复杂计算的验证。在实际场景中，只要存在对隐私数据计算的可验证性需求，理论上都可考虑尝试采用零知识证明技术解决的可行性，但在应用的必要性方面还需考虑实际可操作性和引入的效率问题。

（4）开发工具

目前，为了解决零知识证明技术的广泛应用需求，产生了多个用于实现zk-SNARK零知识证明协议工程化的开源算法库，包括libsnark、bellman、ZoKrates等等。

①libsnark

libsnark是一个基于C++语言的zk-SNARK工程开发算法库，由SCIPR Lab开发和维护，开发者中包含参与多篇zk-SNARK学术论文的共同作者。libsnark实现了近年来多个主流的zk-SNARK论文方案，其中最为常用的包括BCTV14a和Groth16方案。

libsnark实现了zk-SNARK算法的黑盒化，提供高度抽象的编程接口，使开发者无需掌握算法细节即可直接进行工程开发。此外，libsnark还提供了实际应用中的常见基础功能库，可辅助开发者进行复杂证明的组合实现。以在匿名数字货币Zcash中的应用为开端，libsnark奠定了零知识证明技术从理论研究到大规模工程应用的基础。

②bellman

在Zcash项目中，最初采用libsnark算法库实现zk-SNARK零知识证明。在2018年升级到Sapling版本时，由于之前采用的libsnark版本较老，其中关于椭圆曲线和zk-SNARK方案的选择都已不是当时的最优选项，Zcash改为使用自研的bellman算法库。bellman是Zcash团队基于Rust语言实现的zk-SNARK算法库，支持Groth16论文方案，目前主要在Zcash项目中应用。

③ZoKrates

ZoKrates是一个部分基于libsnark、部分采用Rust语言重写的zk-SNARK实现工具，默认支持Groth16方案，开发者需要使用一种自建的脚本语言进行代码编写，目前在实际工程中仅用于在以太坊智能合约上部署支持零知识证明的应用。

2、其他算法

（1）zk-STARK

zk-STARK（Zero-Knowledge Scalable Transparent Arguments of Knowledge，零知识可扩展透明知识论证）[13]是2018年提出的一种通用非交互式零知识证明算法，通过多项式插值等方法将证明计算式转化为证明多项式小于某个度的问题，实现对问题的零知识证明。

zk-SNARK算法主要可分为算术化（Arithmetization）和低度测试（Low Degree Testing, LDT）两部分。算术化过程将待证明问题转化为多项式的形式，具体内容包括生成与R1CS类似的执行轨迹（Execute Trace）并构造多项式约束，然后对执行轨迹进行多项式插值，并与多项式约束进行组合变换，得到确定性的验证多项式；而LDT过程则通过二分法验证证明组合多项式和轨迹多项式小于某个固定的度，确保证明者给出的满足多项式的值是基于有效的多项式计算的，用于防止证明者伪造证明，具体基于FRI（Fast Reed-Solomen Interactive Oracle Proofs of Proximity）协议实现。

zk-STARK与zk-SNARK相比主要有以下异同点：

①相同点

zk-STARK和zk-SNARK均实现了对隐私输入的隐藏；

zk-STARK和zk-SNARK均为基于知识的论证，即在不知道隐私输入的情况下无法生成有效证明；

zk-STARK和zk-SNARK均可实现非交互式协议；

zk-STARK和zk-SNARK均通过将计算式转化为多项式实现零知识证明。

②不同点

zk-STARK具有透明性，即不需要通过由可信第三方完成的可信设置过程生成CRS；

zk-STARK具有可扩展性，即证明过程的耗时与输入大小呈线性关系，但验证过程的耗时仅与输入大小呈对数关系；

zk-STARK生成的证明大小比zk-SNARK大很多。

总的来说，与zk-SNARK相比，zk-STARK不需要通过可信第三方生成CRS，且验证耗时仅与输入大小呈对数关系，但其生成的证明更大。面对区块链等应用场景宝贵的存储资源，zk-SNARK在证明的简洁性方面更胜一筹。

（2）BulletProof

BulletProof[14]零知识证明算法同样于2018年提出，主要用于实现范围证明（Range Proof），目前已在Monero匿名数字货币中应用。

在BulletProof范围证明中，证明者可向验证者证明其拥有的秘密值v在一个确定的范围，而不会泄露关于v的任何信息。此外，通过对范围证明进行组合变换，还可进一步实现大小关系的证明。BulletProof算法具有生成证明小的优点，且同样不需要通过可信设置仪式生成CRS，但其主要功能优势在于范围证明，因此在普遍适用性方面还有待进一步验证。

除以上介绍的算法外，在目前的实际应用中还存在着PLONK、AZTEC等其他可用的新型零知识证明算法。作为通用非交互式零知识证明的应用先驱，zk-SNARK算法的功能更为全面，学术与技术资源更为丰富，实际的工程应用场景也更加广泛。

四、零知识证明应用场景

作为一类经典的密码学原语，零知识证明至今已有三十多年的历史。但是，直至近年来基于区块链的匿名数字货币的诞生，零知识证明技术才开始有了较大规模的应用。目前，零知识证明在工程应用上仍处于起步阶段，且在可信设置、运算效率等方面存在着一些瓶颈，依然还是一项尚未真正成熟的密码学技术。

本章对目前零知识证明技术在区块链、数字货币、安全多方计算等领域的应用场景进行举例分析。

1、在区块链数字货币中的应用

（1）Zcash

Zcash是一种基于区块链的匿名数字货币，起源于Zerocoin协议。2014年，经过效率和匿名性等方面的改进，Zerocoin协议发展为Zerocash协议[15]。2016年，基于Zerocash协议的Zcash数字货币应用项目正式向公众开放。

Zcash采用zk-SNARK零知识证明协议实现了隐蔽交易的功能。在比特币中，需要通过公开在区块链上的交易发送方地址、交易接收方地址以及输入和输出金额来验证交易。而在Zcash中，通过zk-SNARK来证明交易满足有效条件，而不会公开任何有关地址或金额的关键信息。隐蔽交易的发送方通过构建一个证明，从而以足够高的概率来证明交易满足以下条件：

①交易的输入总金额和输出总金额相等；

②交易发送方拥有支配交易金额的私钥；

③支配交易金额的私钥与交易的签名绑定，交易无法被不知道私钥的人篡改。

在Zcash中，隐蔽交易的UTXO（Unspent Transaction Output）被称为Commitment（承诺），而支出一个Commitment对应的金额需要公布一个相应的Nullifier。Zcash节点会保存包含所有已创建的Commitment组成的Merkle树以及所有已公布的Nullifier列表。Commitment和Nullifier通过哈希值存储，防止泄露Commitment的信息以及Commitment和Nullfier的对应关系。

对于输入金额的来源，每次隐蔽交易都会产生一份未使用的金额，以一个Commitment的形式进行公布，其值为接收方地址、交易金额、秘密的交易唯一标识和一个随机串（Random Nounce）的哈希值。

对于输出金额的去向，当隐蔽交易发起时，交易发送方使用支配交易金额的私钥发布一个Nullifier，其值是现有未使用Commitment中交易唯一标识的哈希值，并生成证明其有权使用相应金额的零知识证明。交易发送方需要将私钥对应的公钥和交易唯一标识通过秘密信道发送给交易接收方以完成交易。为了防止双花，Zcash区块链节点会验证该Nullifier不在已经公布的列表中。

进而，隐蔽交易的零知识证明还可以验证以下论断的真实性：

①对于每一份输入金额，都存在一个已公布的Commitment；

②Nullifier和Commitment是被正确计算的；

③不同输出交易的Nullifier不会发生哈希碰撞。

对于每个隐蔽交易，交易发送方通过证明密钥生成输入金额有效性证明，区块链节点通过验证密钥来验证交易发送方的证明。

Zcash通过Trusted Setup公共参数仪式生成零知识证明的证明密钥和验证密钥，并与Zcash网络中的所有参与者共享。2016年10月22日至23日，Zcash举行了可信设置仪式生成zk-SNARK的公共参考串CRS，通过由具有竞争关系的六个参与者参与的多方计算协议，保证CRS的安全生成，除非参与参数生成的所有人共谋，否则被销毁的随机参数无法得到恢复。

（2）Monero

Monero（门罗币）也是一种支持交易隐私保护的数字货币，创始于2014年，其通过密码学技术手段实现了以下两个属性：

①不可链接性（Unlinkability）：无法判断两个交易的接收方是否是同一个人，即保证了交易接收方的匿名性；

②不可追踪性（Untraceability）：无法知道交易的发送方是谁，即保证了交易发送方的匿名性。

Monero主要依赖于以下三种密码学机制：

①一次性密钥（One-Time Key）：每次交易生成不同密钥以隐藏真实的交易接收方；

②环签名（Ring Signature）：将交易发送方的输入与其他人的输入进行混淆签名，外界无法将不同交易进行关联；

③环签名保密交易（Ring Confidential Transaction, RingCT）：隐藏交易金额。

RingCT[16]采用零知识证明技术——Pedersen承诺，可在隐藏交易金额的同时实现区块链的验证，即对交易的输入总金额与输出总金额（包含交易费用）之差是否为0进行零知识证明承诺。

然而，由于基于群代数的密码学存在模运算，无法将小负数与对应模数的大正数进行区分，可能导致伪造币的产生。因此，为了在保护交易金额机密性的同时保证交易金额不为负数，且金额不能过大至与小负数在对应模数上同余，需要对交易的输出金额进行范围证明。最初的范围证明协议基于Borromean环签名技术，其证明大小与范围区间的上限成线性关系，成为了交易的主要负担，影响了区块链的整体效率。

2018年，Monero进行了一次硬分叉升级，引入了BulletProof零知识证明算法以提升交易效率。BulletProof用于取代之前基于环签名的范围证明协议，其产生的证明大小仅与范围区间上限成对数关系，同时可将多个证明进行合并以实现进一步优化，最终将区块链的大小以及交易费用减少70%~80%。

2、在区块链其他场景中的应用——以太坊扩容

以太坊（Ethereum）是一个知名的公有区块链平台，通过在去中心化网络节点上的以太坊虚拟机（Ethereum Virtual Machine, EVM）中运行以图灵完备语言编写的智能合约（Smart Contract），进而承载去中心化应用（Decentrialized Application, DApp）的部署。随着越来越多DApp的部署，以太坊遇到了几乎所有公有链平台所共有的性能瓶颈问题，由此产生了各类针对以太坊的扩容方案。

以太坊扩容方案一般分为第一层（Layer-1）扩容方案和第二层（Layer-2）扩容方案。Layer-1扩容方案是指直接增加链上的交易处理能力，即链上扩容，常见的技术方案有分片（Sharding）和有向无环图（Directed Acyclic Graph, DAG）等；Layer-2扩容方案是指将链上的相当一部分工作量转移到链下完成，常见的技术方案包括状态通道、Plasma、Truebit等。

ZK-Rollup是一类基于zk-SNARK零知识证明的以太坊Layer-2扩容方案，其实现案例为ZK-Sync去信任化扩容及隐私解决方案。ZK-Rollup将链上的账户状态（包含公钥、Nonce和余额）压缩存储在一棵Merkle树中，并将账户状态变更的处理转移到链下，同时通过zk-SNARK零知识证明生成每个交易的有效性证明，保证链下账户状态变更的正确性，具体包括交易的Nonce、金额、费用以及签名等内容的正确性，并将证明结果提交到链上的智能合约中。由于在链上直接处理账户状态变更的成本较高，而仅通过链上的智能合约验证零知识证明结果的成本相对低很多，因此零知识证明的应用可大大提高以太坊的交易处理效率，真正实现扩容的目的。零知识证明技术的引入预计可将以太坊的每秒交易吞吐量从目前的约15TPS提升至主流支付转接清算网络级别的数千TPS。

值得一提的是，以太坊的创始人Vitalik Buterin本人就是一个零知识证明技术的支持者，曾多次在不同场合公开支持zk-SNARK等零知识证明技术在以太坊等区块链平台中进行应用。

3、在安全多方计算中的应用

隐私计算是密码学技术的另一个重要应用领域。基于密码学的安全多方计算（Multi-Party Computation, MPC）方案通常采用混淆电路（Garbled Circuit）、不经意传输（Oblivious Transfer）、同态加密（Homomorphic Encryption）、同态承诺（Homomorphic Commitment）、秘密共享（Secret Sharing）以及零知识证明等技术手段，实现多个参与方之间数据共享计算过程中的隐私保护。从密码学的本质上来说，安全多方计算的定义是在无可信第三方的情况下，若干个互相不信任的参与方使用各自的私有数据安全地计算一个约定函数而不泄露各自原始数据的问题。

在典型的安全多方计算方案中，参与方之间通常会事先约定一个计算框架，并要求双方按照既定的框架执行计算。但是，参与方可能怀疑对方是否使用其私有数据真正进行了计算，因此可引入零知识证明技术用于解决这一计算结果的可信验证问题。具体而言，参与方中的一方在通过混淆电路或同态加密等方法完成安全计算后，除了将计算结果提供给其他参与方外，还可将计算过程转化为零知识证明电路，并采用零知识证明算法生成计算过程的证明结果供其他参与方验证。根据零知识证明协议满足的完备性、可靠性和零知识性三个基本属性，通过这一过程即可在不泄露具体计算数据的情况下，使其他参与方相信计算是按照正确步骤进行的。

五、总结

得益于近年来区块链、数字货币、隐私计算等新兴技术应用的发展，零知识证明这一具有30多年历史的经典密码学技术在最近5到10年又产生了极为丰富的理论与应用成果。在区块链应用中，对于不同参与方的数据交互验证可采用零知识证明技术实现，避免敏感信息的相互泄露；在安全多方计算应用中，参与双方可在通过同态加密等方法保护的隐私计算完成后要求互相提供计算过程的零知识证明结果进行验证，防止虚假计算，同时又不会泄露计算过程中的敏感信息。

总的来说，零知识证明这一“新瓶装旧酒”的密码技术，在目前十分热门的区块链、数字货币、安全多方计算等场景中都有着一定的应用潜力。

参考文献

[1] Quisquater J J, Quisquater M, Quisquater M, et al. How to explain zero-knowledge protocols to your children[C]//Conference on the Theory and Application of Cryptology. Springer, New York, NY, 1989: 628-631.

[2] Goldwasser S, Micali S, Rackoff C. The knowledge complexity of interactive proof systems[J]. SIAM Journal on computing, 1989, 18(1): 186-208.

[3] Gradwohl R, Naor M, Pinkas B, et al. Cryptographic and physical zero-knowledge proof systems for solutions of sudoku puzzles[J]. Theory of Computing Systems, 2009,44(2): 245-268.

[4] Goldreich O, Micali S, Wigderson A. Proofs that yield nothing but their validity or all languages in NP have zero-knowledge proof systems[J]. Journal of the ACM (JACM), 1991, 38(3): 690-728.

[5] Schnorr C P. Efficient signature generation by smart cards[J]. Journal of cryptology,1991, 4(3): 161-174.

[6] BlumM, Feldman P, Micali S. Non-interactive zero-knowledge and its applications[C]//Proceedings of the twentieth annual ACM symposium on Theory of computing. 1988: 103-112.

[7] Fiat A, Shamir A. How to prove yourself: Practical solutions to identification andsignature problems[C]//Conference on the theory and application of cryptographic techniques. Springer, Berlin, Heidelberg, 1986: 186-194.

[8] Bitansky N, Canetti R, Chiesa A, et al. From extractable collision resistance tosuccinct non-interactive arguments of knowledge, and back again[C]//Proceedings of the 3rd Innovations in Theoretical Computer Science Conference. 2012: 326-349.

[9] Groth J. Short pairing-based non-interactive zero-knowledge arguments[C]//International Conference on the Theory and Application of Cryptology and Information Security. Springer, Berlin, Heidelberg, 2010: 321-340.

[10] Parno B, Howell J, Gentry C, et al. Pinocchio: Nearly practical verifiable computation[C]//2013 IEEE Symposium on Security and Privacy. IEEE, 2013: 238-252.

[11] Ben-Sasson E, Chiesa A, Tromer E, et al. Succinct non-interactive zero knowledge for a von Neumann architecture[C]//23rd USENIX Security Symposium (USENIX Security 14). 2014: 781-796.

[12] Groth J. On the size of pairing-basednon-interactive arguments[C]//Annual international conference on the theory andapplications of cryptographic techniques. Springer, Berlin, Heidelberg, 2016: 305-326.

[13] Ben-Sasson E, Bentov I, Horesh Y, et al. Scalable, transparent, and post-quantum secure computational integrity[J]. IACR Cryptology ePrint Archive, 2018, 2018: 46.

[14] Bünz B, Bootle J, Boneh D, et al. Bulletproofs: Short proofs for confidential transactions and more[C]//2018 IEEE Symposium on Security and Privacy (SP). IEEE, 2018: 315-334.

[15] Sasson E B, Chiesa A, Garman C, et al. Zerocash: Decentralized anonymous payments from bitcoin[C]//2014 IEEE Symposiumon Security and Privacy. IEEE, 2014: 459-474.

[16] Noether S, Mackenzie A. Ring confidential transactions[J]. Ledger, 2016, 1: 1-18.

*本文作者：狴犴安全团队，转载请注明来自FreeBuf.COM